红帽全球峰会此内容没有您所选择的语言版本。
Chapter 31. Examples provided with Red Hat build of OptaPlanner
Several Red Hat build of OptaPlanner examples are shipped with Red Hat Process Automation Manager. You can review the code for examples and modify it as necessary to suit your needs.
Red Hat does not provide support for the example code included in the Red Hat Process Automation Manager distribution.
Some of the OptaPlanner examples solve problems that are presented in academic contests. The Contest column in the following table lists the contests. It also identifies an example as being either realistic or unrealistic for the purpose of a contest. A realistic contest is an official, independent contest that meets the following standards:
- Clearly defined real-world use cases
- Real-world constraints
- Multiple real-world datasets
- Reproducible results within a specific time limit on specific hardware
- Serious participation from the academic and/or enterprise Operations Research community.
Realistic contests provide an objective comparison of OptaPlanner with competitive software and academic research.
| Example | Domain | Size | Contest | Directory name |
|---|---|---|---|---|
| 1 entity class (1 variable) |
Entity ⇐
Value ⇐
Search space ⇐ | Pointless (cheatable) |
| |
| 1 entity class (1 variable) |
Entity ⇐
Value ⇐
Search space ⇐ | No (Defined by us) |
| |
| 1 entity class (1 chained variable) |
Entity ⇐
Value ⇐
Search space ⇐ | Unrealistic TSP web |
| |
| 1 entity class (1 variable) |
Entity ⇐
Value ⇐
Search space ⇐ | No (Defined by us) |
| |
| 1 entity class (2 variables) |
Entity ⇐
Value ⇐
Search space ⇐ | No (Defined by us) |
| |
| 1 entity class (2 variables) |
Entity ⇐
Value ⇐
Search space ⇐ | Realistic ITC 2007 track 3 |
| |
| 1 entity class (1 variable) |
Entity ⇐
Value ⇐
Search space ⇐ | Nearly realistic ROADEF 2012 |
| |
| 1 entity class (1 chained variable) 1 shadow entity class (1 automatic shadow variable) |
Entity ⇐
Value ⇐
Search space ⇐ | Unrealistic VRP web |
| |
| Vehicle routing with time windows | All of Vehicle routing (1 shadow variable) |
Entity ⇐
Value ⇐
Search space ⇐ | Unrealistic VRP web |
|
| 1 entity class (2 variables) (1 shadow variable) |
Entity ⇐
Value ⇐
Search space ⇐ | Nearly realistic MISTA 2013 |
| |
| 1 entity class (1 chained variable) (1 shadow variable) 1 shadow entity class (1 automatic shadow variable) |
Entity ⇐
Value ⇐
Search space ⇐ | No Defined by us |
| |
| 2 entity classes (same hierarchy) (2 variables) |
Entity ⇐
Value ⇐
Search space ⇐ | Realistic ITC 2007 track 1 |
| |
| 1 entity class (1 variable) |
Entity ⇐
Value ⇐
Search space ⇐ | Realistic INRC 2010 |
| |
| 1 entity class (1 variable) |
Entity ⇐
Value ⇐
Search space ⇐ | Unrealistic TTP |
| |
| 1 entity class (2 variables) |
Entity ⇐
Value ⇐
Search space ⇐ | Nearly realistic ICON Energy |
| |
| 1 entity class (1 variable) |
Entity ⇐
Value =
Search space ⇐ | No Defined by us |
| |
| 1 entity class (2 variables) |
Entity ⇐
Value ⇐
Search space ⇐ | No Defined by us |
| |
| 1 entity class (1 chained variable) (4 shadow variables) 1 shadow entity class (1 automatic shadow variable) |
Entity ⇐
Value ⇐
Search space ⇐ | No Defined by us |
| |
| 1 entity class (1 variable) 1 shadow entity class (1 automatic shadow variable) |
Entity ⇐
Value ⇐
Search space ⇐ | No Defined by us |
|
31.1. N queens
Place n queens on a n sized chessboard so that no two queens can attack each other. The most common n queens puzzle is the eight queens puzzle, with n = 8:
Constraints:
- Use a chessboard of n columns and n rows.
- Place n queens on the chessboard.
- No two queens can attack each other. A queen can attack any other queen on the same horizontal, vertical, or diagonal line.
This documentation heavily uses the four queens puzzle as the primary example.
A proposed solution could be:
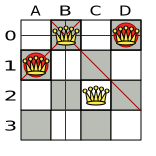
Figure 31.1. A wrong solution for the Four queens puzzle
The above solution is wrong because queens A1 and B0 can attack each other (so can queens B0 and D0). Removing queen B0 would respect the "no two queens can attack each other" constraint, but would break the "place n queens" constraint.
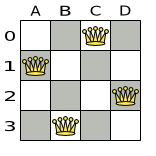
Below is a correct solution:
Figure 31.2. A correct solution for the Four queens puzzle
All the constraints have been met, so the solution is correct.
Note that most n queens puzzles have multiple correct solutions. We will focus on finding a single correct solution for a given n, not on finding the number of possible correct solutions for a given n.
Problem size
The implementation of the n queens example has not been optimized because it functions as a beginner example. Nevertheless, it can easily handle 64 queens. With a few changes it has been shown to easily handle 5000 queens and more.
31.1.1. Domain model for N queens
This example uses the domain model to solve the four queens problem.
Creating a Domain Model
A good domain model will make it easier to understand and solve your planning problem.
This is the domain model for the n queens example:
Copy to Clipboard Copied! Toggle word wrap Toggle overflow Copy to Clipboard Copied! Toggle word wrap Toggle overflow Copy to Clipboard Copied! Toggle word wrap Toggle overflow Calculating the Search Space.
A
Queeninstance has aColumn(for example: 0 is column A, 1 is column B, …) and aRow(its row, for example: 0 is row 0, 1 is row 1, …).The ascending diagonal line and the descending diagonal line can be calculated based on the column and the row.
The column and row indexes start from the upper left corner of the chessboard.
Copy to Clipboard Copied! Toggle word wrap Toggle overflow Finding the Solution
A single
NQueensinstance contains a list of allQueeninstances. It is theSolutionimplementation which will be supplied to, solved by, and retrieved from the Solver.
Notice that in the four queens example, NQueens’s getN() method will always return four.
Figure 31.3. A solution for Four Queens
| columnIndex | rowIndex | ascendingDiagonalIndex (columnIndex + rowIndex) | descendingDiagonalIndex (columnIndex - rowIndex) | |
|---|---|---|---|---|
| A1 | 0 | 1 | 1 (**) | -1 |
| B0 | 1 | 0 (*) | 1 (**) | 1 |
| C2 | 2 | 2 | 4 | 0 |
| D0 | 3 | 0 (*) | 3 | 3 |
When two queens share the same column, row or diagonal line, such as (*) and (**), they can attack each other.
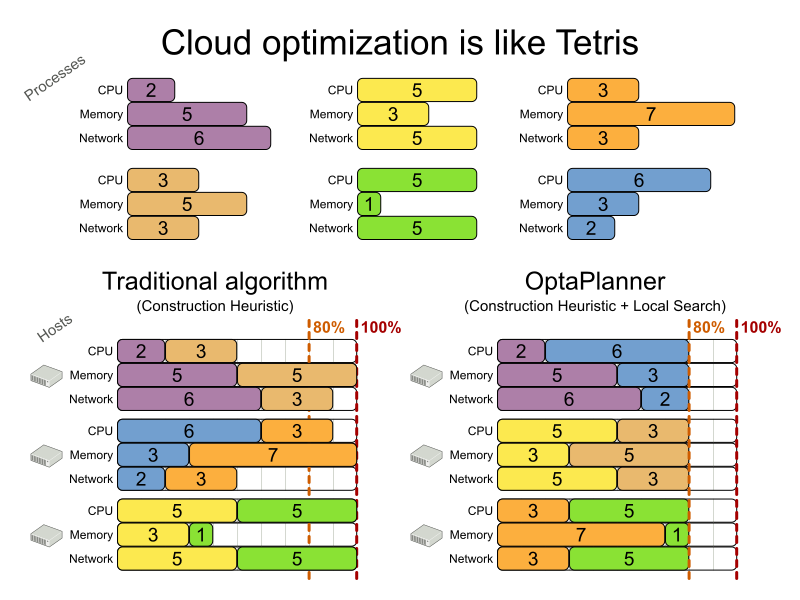
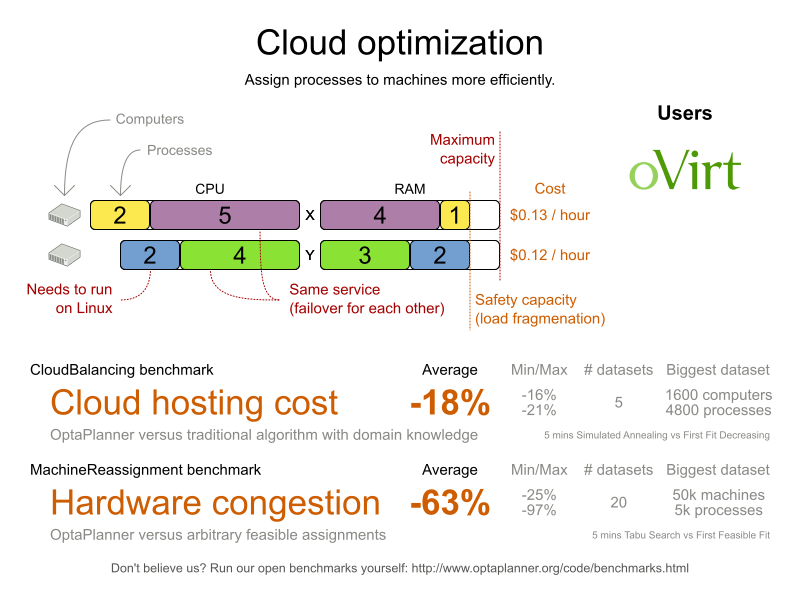
31.2. Cloud balancing
For information about this example, see Red Hat build of OptaPlanner quick start guides.
Given a list of cities, find the shortest tour for a salesman that visits each city exactly once.
The problem is defined by Wikipedia. It is one of the most intensively studied problems in computational mathematics. Yet, in the real world, it is often only part of a planning problem, along with other constraints, such as employee shift rostering constraints.
Problem size
dj38 has 38 cities with a search space of 10^43. europe40 has 40 cities with a search space of 10^46. st70 has 70 cities with a search space of 10^98. pcb442 has 442 cities with a search space of 10^976. lu980 has 980 cities with a search space of 10^2504.
dj38 has 38 cities with a search space of 10^43.
europe40 has 40 cities with a search space of 10^46.
st70 has 70 cities with a search space of 10^98.
pcb442 has 442 cities with a search space of 10^976.
lu980 has 980 cities with a search space of 10^2504.Problem difficulty
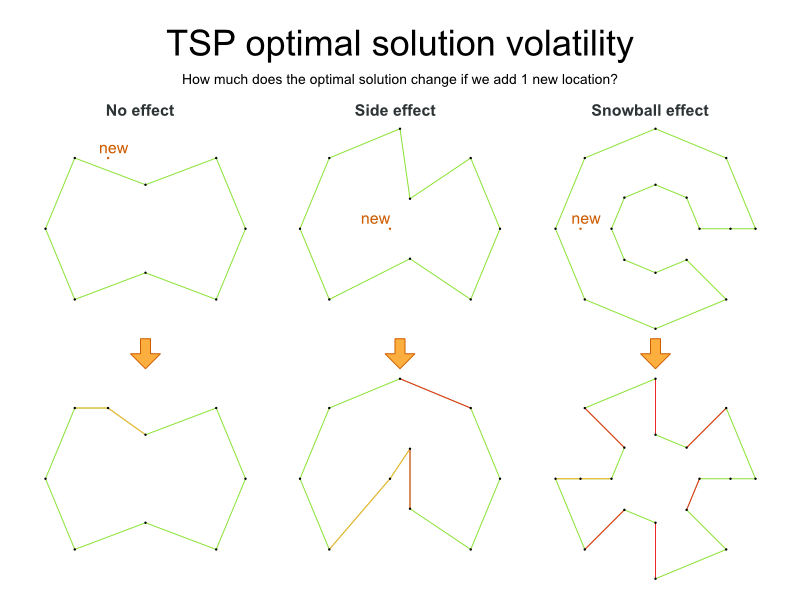
Despite TSP’s simple definition, the problem is surprisingly hard to solve. Because it is an NP-hard problem (like most planning problems), the optimal solution for a specific problem dataset can change a lot when that problem dataset is slightly altered:
31.4. Tennis club scheduling
Every week the tennis club has four teams playing round robin against each other. Assign those four spots to the teams fairly.
Hard constraints:
- Conflict: A team can only play once per day.
- Unavailability: Some teams are unavailable on some dates.
Medium constraints:
- Fair assignment: All teams should play an (almost) equal number of times.
Soft constraints:
- Evenly confrontation: Each team should play against every other team an equal number of times.
Problem size
munich-7teams has 7 teams, 18 days, 12 unavailabilityPenalties and 72 teamAssignments with a search space of 10^60.
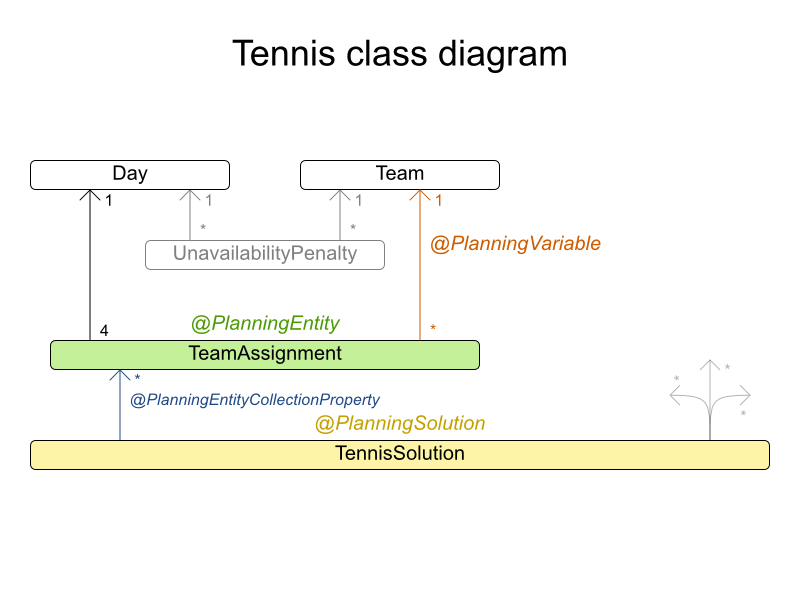
munich-7teams has 7 teams, 18 days, 12 unavailabilityPenalties and 72 teamAssignments with a search space of 10^60.Figure 31.4. Domain model
31.5. Meeting scheduling
Assign each meeting to a starting time and a room. Meetings have different durations.
Hard constraints:
- Room conflict: two meetings must not use the same room at the same time.
- Required attendance: A person cannot have two required meetings at the same time.
- Required room capacity: A meeting must not be in a room that doesn’t fit all of the meeting’s attendees.
- Start and end on same day: A meeting shouldn’t be scheduled over multiple days.
Medium constraints:
- Preferred attendance: A person cannot have two preferred meetings at the same time, nor a preferred and a required meeting at the same time.
Soft constraints:
- Sooner rather than later: Schedule all meetings as soon as possible.
- A break between meetings: Any two meetings should have at least one time grain break between them.
- Overlapping meetings: To minimize the number of meetings in parallel so people don’t have to choose one meeting over the other.
- Assign larger rooms first: If a larger room is available any meeting should be assigned to that room in order to accommodate as many people as possible even if they haven’t signed up to that meeting.
- Room stability: If a person has two consecutive meetings with two or less time grains break between them they better be in the same room.
Problem size
50meetings-160timegrains-5rooms has 50 meetings, 160 timeGrains and 5 rooms with a search space of 10^145. 100meetings-320timegrains-5rooms has 100 meetings, 320 timeGrains and 5 rooms with a search space of 10^320. 200meetings-640timegrains-5rooms has 200 meetings, 640 timeGrains and 5 rooms with a search space of 10^701. 400meetings-1280timegrains-5rooms has 400 meetings, 1280 timeGrains and 5 rooms with a search space of 10^1522. 800meetings-2560timegrains-5rooms has 800 meetings, 2560 timeGrains and 5 rooms with a search space of 10^3285.
50meetings-160timegrains-5rooms has 50 meetings, 160 timeGrains and 5 rooms with a search space of 10^145.
100meetings-320timegrains-5rooms has 100 meetings, 320 timeGrains and 5 rooms with a search space of 10^320.
200meetings-640timegrains-5rooms has 200 meetings, 640 timeGrains and 5 rooms with a search space of 10^701.
400meetings-1280timegrains-5rooms has 400 meetings, 1280 timeGrains and 5 rooms with a search space of 10^1522.
800meetings-2560timegrains-5rooms has 800 meetings, 2560 timeGrains and 5 rooms with a search space of 10^3285.Schedule each lecture into a timeslot and into a room.
Hard constraints:
- Teacher conflict: A teacher must not have two lectures in the same period.
- Curriculum conflict: A curriculum must not have two lectures in the same period.
- Room occupancy: Two lectures must not be in the same room in the same period.
- Unavailable period (specified per dataset): A specific lecture must not be assigned to a specific period.
Soft constraints:
- Room capacity: A room’s capacity should not be less than the number of students in its lecture.
- Minimum working days: Lectures of the same course should be spread out into a minimum number of days.
- Curriculum compactness: Lectures belonging to the same curriculum should be adjacent to each other (so in consecutive periods).
- Room stability: Lectures of the same course should be assigned to the same room.
The problem is defined by the International Timetabling Competition 2007 track 3.
Problem size
Figure 31.5. Domain model
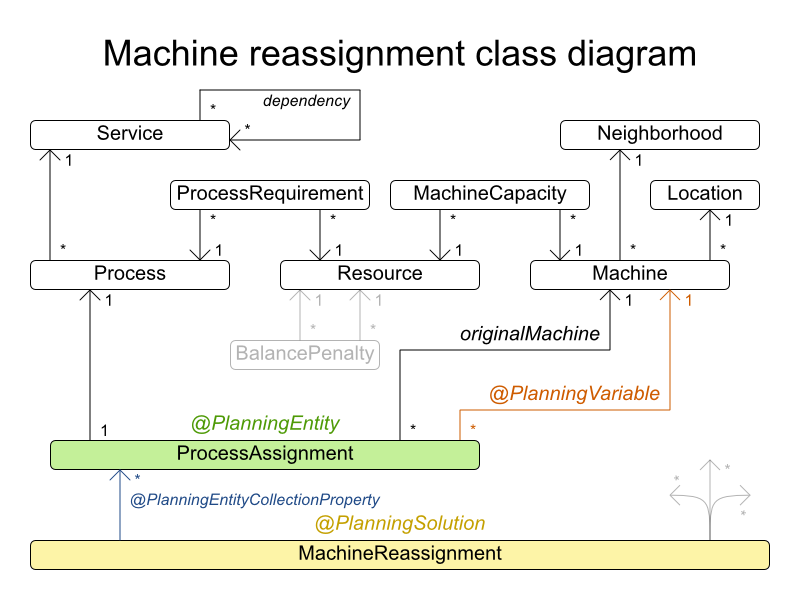
31.7. Machine reassignment (Google ROADEF 2012)
Assign each process to a machine. All processes already have an original (unoptimized) assignment. Each process requires an amount of each resource (such as CPU or RAM). This is a more complex version of the Cloud Balancing example.
Hard constraints:
- Maximum capacity: The maximum capacity for each resource for each machine must not be exceeded.
- Conflict: Processes of the same service must run on distinct machines.
- Spread: Processes of the same service must be spread out across locations.
- Dependency: The processes of a service depending on another service must run in the neighborhood of a process of the other service.
- Transient usage: Some resources are transient and count towards the maximum capacity of both the original machine as the newly assigned machine.
Soft constraints:
- Load: The safety capacity for each resource for each machine should not be exceeded.
- Balance: Leave room for future assignments by balancing the available resources on each machine.
- Process move cost: A process has a move cost.
- Service move cost: A service has a move cost.
- Machine move cost: Moving a process from machine A to machine B has another A-B specific move cost.
The problem is defined by the Google ROADEF/EURO Challenge 2012.
Figure 31.6. Value proposition
Problem size
Figure 31.7. Domain model
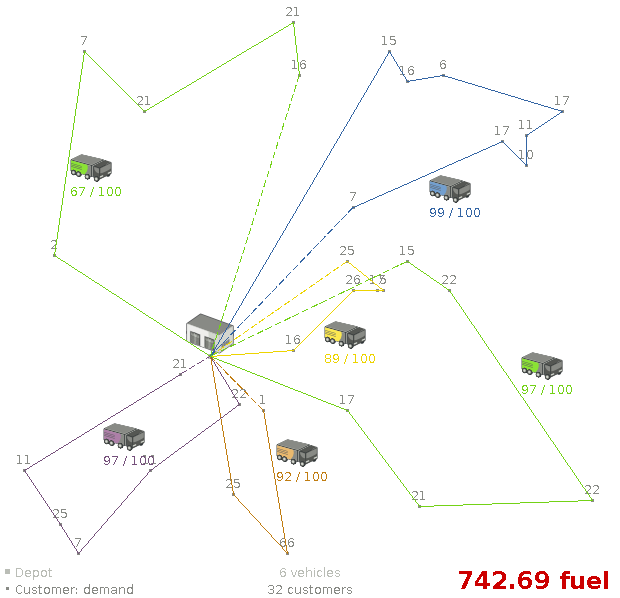
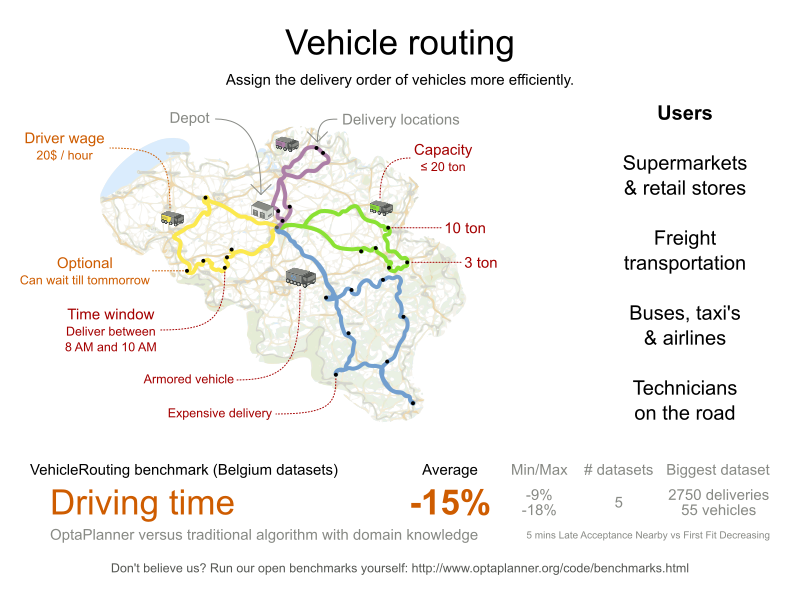
31.8. Vehicle routing
Using a fleet of vehicles, pick up the objects of each customer and bring them to the depot. Each vehicle can service multiple customers, but it has a limited capacity.
Besides the basic case (CVRP), there is also a variant with time windows (CVRPTW).
Hard constraints:
- Vehicle capacity: a vehicle cannot carry more items then its capacity.
Time windows (only in CVRPTW):
- Travel time: Traveling from one location to another takes time.
- Customer service duration: a vehicle must stay at the customer for the length of the service duration.
- Customer ready time: a vehicle may arrive before the customer’s ready time, but it must wait until the ready time before servicing.
- Customer due time: a vehicle must arrive on time, before the customer’s due time.
Soft constraints:
- Total distance: minimize the total distance driven (fuel consumption) of all vehicles.
The capacitated vehicle routing problem (CVRP) and its time-windowed variant (CVRPTW) are defined by the VRP web.
Figure 31.8. Value proposition
Problem size
CVRP instances (without time windows):
CVRPTW instances (with time windows):
31.8.1. Domain model for Vehicle routing
The vehicle routing with timewindows domain model makes heavily use of the shadow variable feature. This allows it to express its constraints more naturally, because properties such as arrivalTime and departureTime, are directly available on the domain model.
Road Distances Instead of Air Distances
In the real world, vehicles cannot follow a straight line from location to location: they have to use roads and highways. From a business point of view, this matters a lot:
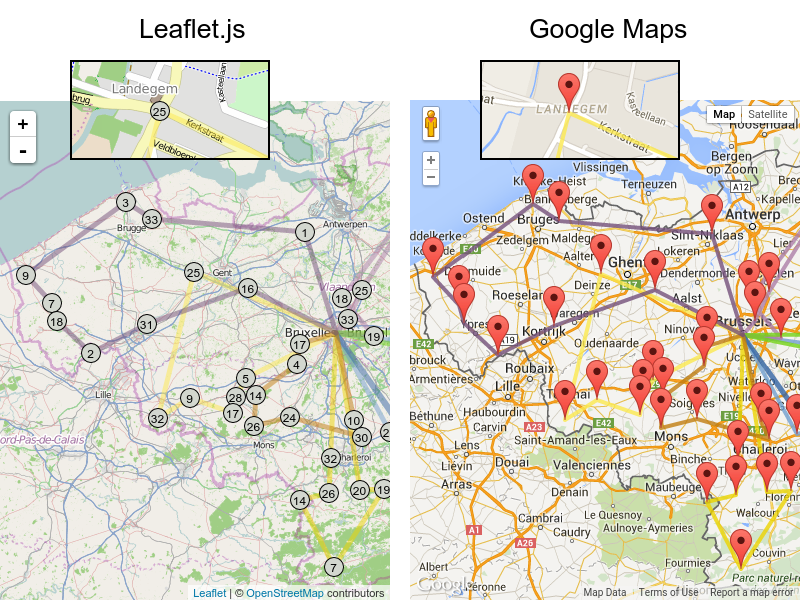
For the optimization algorithm, this does not matter much, as long as the distance between two points can be looked up (and are preferably precalculated). The road cost does not even need to be a distance, it can also be travel time, fuel cost, or a weighted function of those. There are several technologies available to precalculate road costs, such as GraphHopper (embeddable, offline Java engine), Open MapQuest (web service) and Google Maps Client API (web service).
There are also several technologies to render it, such as Leaflet and Google Maps for developers.
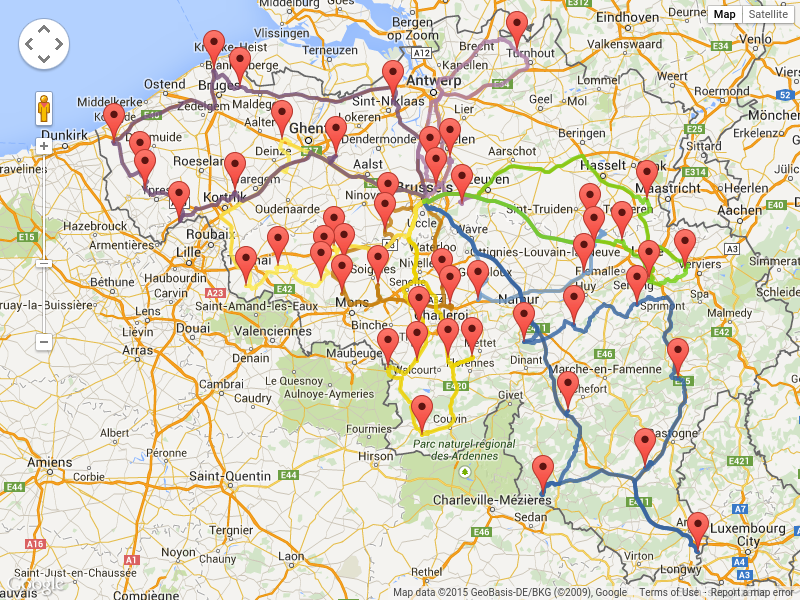
It is even possible to render the actual road routes with GraphHopper or Google Map Directions, but because of route overlaps on highways, it can become harder to see the standstill order:
Take special care that the road costs between two points use the same optimization criteria as the one used in Planner. For example, GraphHopper etc will by default return the fastest route, not the shortest route. Don’t use the km (or miles) distances of the fastest GPS routes to optimize the shortest trip in Planner: this leads to a suboptimal solution as shown below:
Contrary to popular belief, most users do not want the shortest route: they want the fastest route instead. They prefer highways over normal roads. They prefer normal roads over dirt roads. In the real world, the fastest and shortest route are rarely the same.
31.9. Project job scheduling
Schedule all jobs in time and execution mode to minimize project delays. Each job is part of a project. A job can be executed in different ways: each way is an execution mode that implies a different duration but also different resource usages. This is a form of flexible job shop scheduling.
Hard constraints:
- Job precedence: a job can only start when all its predecessor jobs are finished.
Resource capacity: do not use more resources than available.
- Resources are local (shared between jobs of the same project) or global (shared between all jobs)
- Resources are renewable (capacity available per day) or nonrenewable (capacity available for all days)
Medium constraints:
- Total project delay: minimize the duration (makespan) of each project.
Soft constraints:
- Total makespan: minimize the duration of the whole multi-project schedule.
The problem is defined by the MISTA 2013 challenge.
Problem size
31.10. Task assigning
Assign each task to a spot in an employee’s queue. Each task has a duration which is affected by the employee’s affinity level with the task’s customer.
Hard constraints:
- Skill: Each task requires one or more skills. The employee must possess all these skills.
Soft level 0 constraints:
- Critical tasks: Complete critical tasks first, sooner than major and minor tasks.
Soft level 1 constraints:
Minimize makespan: Reduce the time to complete all tasks.
- Start with the longest working employee first, then the second longest working employee and so forth, to create fairness and load balancing.
Soft level 2 constraints:
- Major tasks: Complete major tasks as soon as possible, sooner than minor tasks.
Soft level 3 constraints:
- Minor tasks: Complete minor tasks as soon as possible.
Figure 31.9. Value proposition
Problem size
24tasks-8employees has 24 tasks, 6 skills, 8 employees, 4 task types and 4 customers with a search space of 10^30. 50tasks-5employees has 50 tasks, 5 skills, 5 employees, 10 task types and 10 customers with a search space of 10^69. 100tasks-5employees has 100 tasks, 5 skills, 5 employees, 20 task types and 15 customers with a search space of 10^164. 500tasks-20employees has 500 tasks, 6 skills, 20 employees, 100 task types and 60 customers with a search space of 10^1168.
24tasks-8employees has 24 tasks, 6 skills, 8 employees, 4 task types and 4 customers with a search space of 10^30.
50tasks-5employees has 50 tasks, 5 skills, 5 employees, 10 task types and 10 customers with a search space of 10^69.
100tasks-5employees has 100 tasks, 5 skills, 5 employees, 20 task types and 15 customers with a search space of 10^164.
500tasks-20employees has 500 tasks, 6 skills, 20 employees, 100 task types and 60 customers with a search space of 10^1168.Figure 31.10. Domain model
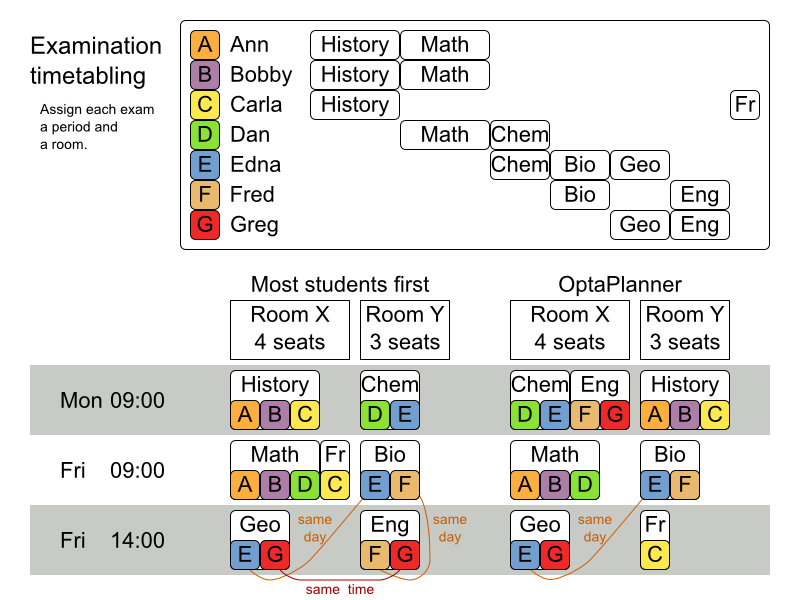
31.11. Exam timetabling (ITC 2007 track 1 - Examination)
Schedule each exam into a period and into a room. Multiple exams can share the same room during the same period.
Hard constraints:
- Exam conflict: Two exams that share students must not occur in the same period.
- Room capacity: A room’s seating capacity must suffice at all times.
- Period duration: A period’s duration must suffice for all of its exams.
Period related hard constraints (specified per dataset):
- Coincidence: Two specified exams must use the same period (but possibly another room).
- Exclusion: Two specified exams must not use the same period.
- After: A specified exam must occur in a period after another specified exam’s period.
Room related hard constraints (specified per dataset):
- Exclusive: One specified exam should not have to share its room with any other exam.
Soft constraints (each of which has a parametrized penalty):
- The same student should not have two exams in a row.
- The same student should not have two exams on the same day.
- Period spread: Two exams that share students should be a number of periods apart.
- Mixed durations: Two exams that share a room should not have different durations.
- Front load: Large exams should be scheduled earlier in the schedule.
- Period penalty (specified per dataset): Some periods have a penalty when used.
- Room penalty (specified per dataset): Some rooms have a penalty when used.
It uses large test data sets of real-life universities.
The problem is defined by the International Timetabling Competition 2007 track 1. Geoffrey De Smet finished 4th in that competition with a very early version of Planner. Many improvements have been made since then.
Problem Size
31.11.1. Domain model for Exam timetabling
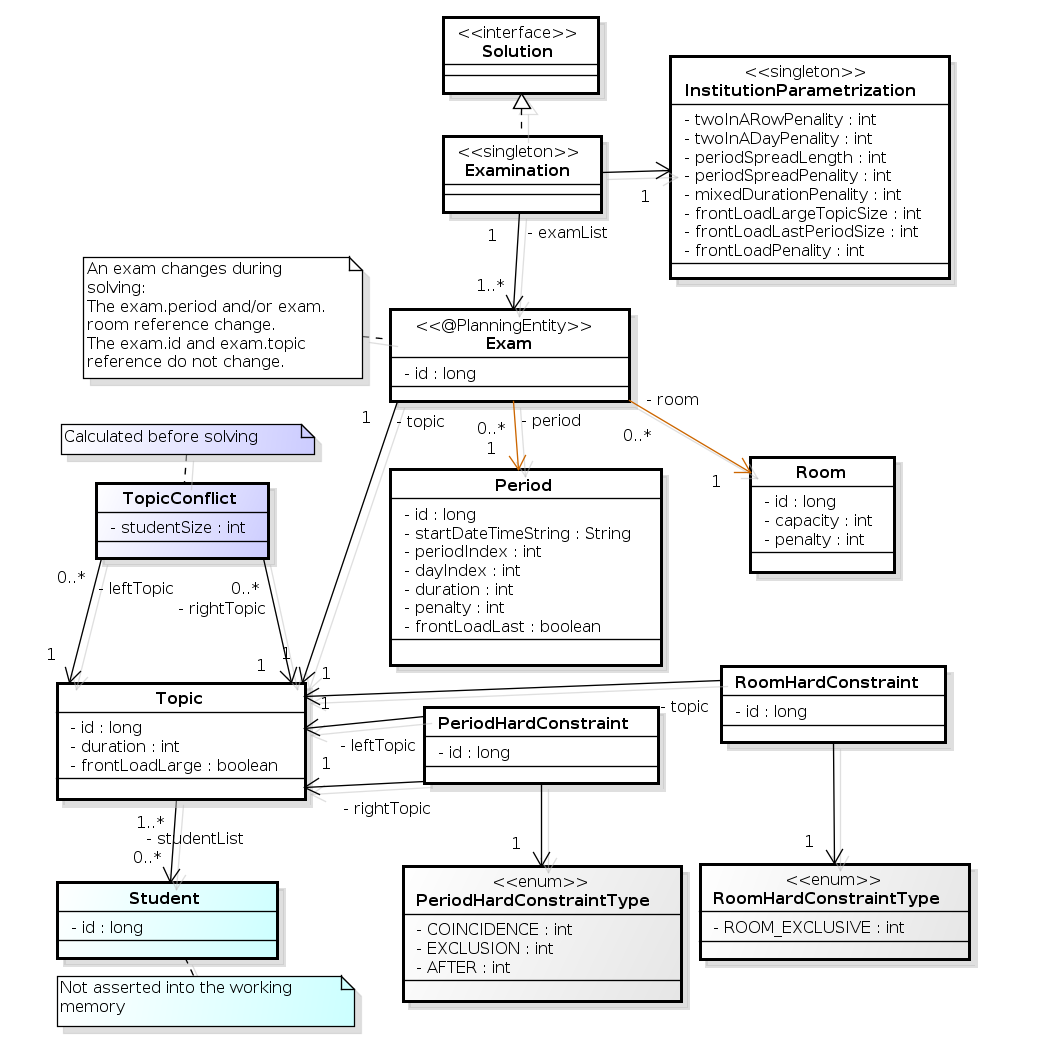
The following diagram shows the main examination domain classes:
Figure 31.11. Examination domain class diagram
Notice that we’ve split up the exam concept into an Exam class and a Topic class. The Exam instances change during solving (this is the planning entity class), when their period or room property changes. The Topic, Period and Room instances never change during solving (these are problem facts, just like some other classes).
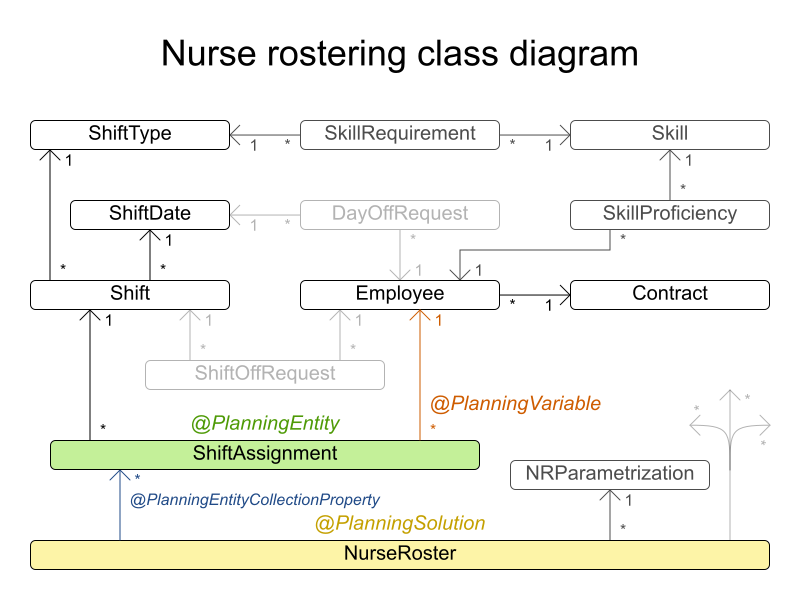
31.12. Nurse rostering (INRC 2010)
For each shift, assign a nurse to work that shift.
Hard constraints:
- No unassigned shifts (built-in): Every shift need to be assigned to an employee.
- Shift conflict: An employee can have only one shift per day.
Soft constraints:
Contract obligations. The business frequently violates these, so they decided to define these as soft constraints instead of hard constraints.
- Minimum and maximum assignments: Each employee needs to work more than x shifts and less than y shifts (depending on their contract).
- Minimum and maximum consecutive working days: Each employee needs to work between x and y days in a row (depending on their contract).
- Minimum and maximum consecutive free days: Each employee needs to be free between x and y days in a row (depending on their contract).
- Minimum and maximum consecutive working weekends: Each employee needs to work between x and y weekends in a row (depending on their contract).
- Complete weekends: Each employee needs to work every day in a weekend or not at all.
- Identical shift types during weekend: Each weekend shift for the same weekend of the same employee must be the same shift type.
- Unwanted patterns: A combination of unwanted shift types in a row. For example: a late shift followed by an early shift followed by a late shift.
Employee wishes:
- Day on request: An employee wants to work on a specific day.
- Day off request: An employee does not want to work on a specific day.
- Shift on request: An employee wants to be assigned to a specific shift.
- Shift off request: An employee does not want to be assigned to a specific shift.
- Alternative skill: An employee assigned to a skill should have a proficiency in every skill required by that shift.
The problem is defined by the International Nurse Rostering Competition 2010.
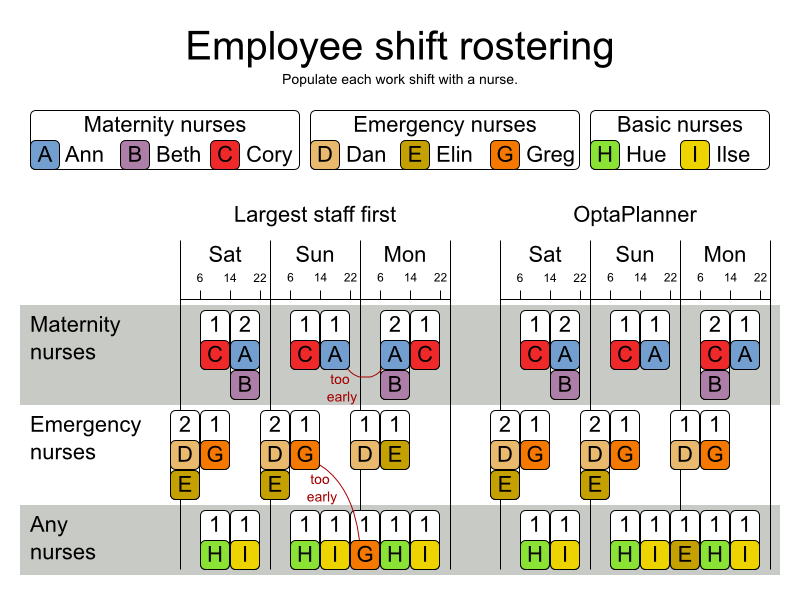
Figure 31.12. Value proposition
Problem size
There are three dataset types:
- sprint: must be solved in seconds.
- medium: must be solved in minutes.
- long: must be solved in hours.
Figure 31.13. Domain model
31.13. Traveling tournament problem (TTP)
Schedule matches between n teams.
Hard constraints:
- Each team plays twice against every other team: once home and once away.
- Each team has exactly one match on each timeslot.
- No team must have more than three consecutive home or three consecutive away matches.
- No repeaters: no two consecutive matches of the same two opposing teams.
Soft constraints:
- Minimize the total distance traveled by all teams.
The problem is defined on Michael Trick’s website (which contains the world records too).
Problem size
31.14. Cheap time scheduling
Schedule all tasks in time and on a machine to minimize power cost. Power prices differs in time. This is a form of job shop scheduling.
Hard constraints:
- Start time limits: Each task must start between its earliest start and latest start limit.
- Maximum capacity: The maximum capacity for each resource for each machine must not be exceeded.
- Startup and shutdown: Each machine must be active in the periods during which it has assigned tasks. Between tasks it is allowed to be idle to avoid startup and shutdown costs.
Medium constraints:
Power cost: Minimize the total power cost of the whole schedule.
- Machine power cost: Each active or idle machine consumes power, which infers a power cost (depending on the power price during that time).
- Task power cost: Each task consumes power too, which infers a power cost (depending on the power price during its time).
- Machine startup and shutdown cost: Every time a machine starts up or shuts down, an extra cost is inflicted.
Soft constraints (addendum to the original problem definition):
- Start early: Prefer starting a task sooner rather than later.
The problem is defined by the ICON challenge.
Problem size
Decide the relative quantity to invest in each asset class.
Hard constraints:
Risk maximum: the total standard deviation must not be higher than the standard deviation maximum.
- Total standard deviation calculation takes asset class correlations into account by applying Markowitz Portfolio Theory.
- Region maximum: Each region has a quantity maximum.
- Sector maximum: Each sector has a quantity maximum.
Soft constraints:
- Maximize expected return.
Problem size
de_smet_1 has 1 regions, 3 sectors and 11 asset classes with a search space of 10^4. irrinki_1 has 2 regions, 3 sectors and 6 asset classes with a search space of 10^3.
de_smet_1 has 1 regions, 3 sectors and 11 asset classes with a search space of 10^4.
irrinki_1 has 2 regions, 3 sectors and 6 asset classes with a search space of 10^3.Larger datasets have not been created or tested yet, but should not pose a problem. A good source of data is this Asset Correlation website.
31.16. Conference scheduling
Assign each conference talk to a timeslot and a room. Timeslots can overlap. Read/write to/from an *.xlsx file that can be edited with LibreOffice or Excel too.
Hard constraints:
- Talk type of timeslot: The type of a talk must match the timeslot’s talk type.
- Room unavailable timeslots: A talk’s room must be available during the talk’s timeslot.
- Room conflict: Two talks can’t use the same room during overlapping timeslots.
- Speaker unavailable timeslots: Every talk’s speaker must be available during the talk’s timeslot.
- Speaker conflict: Two talks can’t share a speaker during overlapping timeslots.
Generic purpose timeslot and room tags
- Speaker required timeslot tag: If a speaker has a required timeslot tag, then all his/her talks must be assigned to a timeslot with that tag.
- Speaker prohibited timeslot tag: If a speaker has a prohibited timeslot tag, then all his/her talks cannot be assigned to a timeslot with that tag.
- Talk required timeslot tag: If a talk has a required timeslot tag, then it must be assigned to a timeslot with that tag.
- Talk prohibited timeslot tag: If a talk has a prohibited timeslot tag, then it cannot be assigned to a timeslot with that tag.
- Speaker required room tag: If a speaker has a required room tag, then all his/her talks must be assigned to a room with that tag.
- Speaker prohibited room tag: If a speaker has a prohibited room tag, then all his/her talks cannot be assigned to a room with that tag.
- Talk required room tag: If a talk has a required room tag, then it must be assigned to a room with that tag.
- Talk prohibited room tag: If a talk has a prohibited room tag, then it cannot be assigned to a room with that tag.
- Talk mutually-exclusive-talks tag: Talks that share such a tag must not be scheduled in overlapping timeslots.
- Talk prerequisite talks: A talk must be scheduled after all its prerequisite talks.
Soft constraints:
- Theme track conflict: Minimize the number of talks that share a same theme tag during overlapping timeslots.
- Sector conflict: Minimize the number of talks that share a same sector tag during overlapping timeslots.
- Content audience level flow violation: For every content tag, schedule the introductory talks before the advanced talks.
- Audience level diversity: For every timeslot, maximize the number of talks with a different audience level.
- Language diversity: For every timeslot, maximize the number of talks with a different language.
Generic purpose timeslot and room tags
- Speaker preferred timeslot tag: If a speaker has a preferred timeslot tag, then all his/her talks should be assigned to a timeslot with that tag.
- Speaker undesired timeslot tag: If a speaker has an undesired timeslot tag, then all his/her talks should not be assigned to a timeslot with that tag.
- Talk preferred timeslot tag: If a talk has a preferred timeslot tag, then it should be assigned to a timeslot with that tag.
- Talk undesired timeslot tag: If a talk has an undesired timeslot tag, then it should not be assigned to a timeslot with that tag.
- Speaker preferred room tag: If a speaker has a preferred room tag, then all his/her talks should be assigned to a room with that tag.
- Speaker undesired room tag: If a speaker has an undesired room tag, then all his/her talks should not be assigned to a room with that tag.
- Talk preferred room tag: If a talk has a preferred room tag, then it should be assigned to a room with that tag.
- Talk undesired room tag: If a talk has an undesired room tag, then it should not be assigned to a room with that tag.
- Same day talks: All talks that share a same theme tag or content tag should be scheduled in the minimum number of days (ideally in the same day).
Figure 31.14. Value proposition
Problem size
18talks-6timeslots-5rooms has 18 talks, 6 timeslots and 5 rooms with a search space of 10^26. 36talks-12timeslots-5rooms has 36 talks, 12 timeslots and 5 rooms with a search space of 10^64. 72talks-12timeslots-10rooms has 72 talks, 12 timeslots and 10 rooms with a search space of 10^149. 108talks-18timeslots-10rooms has 108 talks, 18 timeslots and 10 rooms with a search space of 10^243. 216talks-18timeslots-20rooms has 216 talks, 18 timeslots and 20 rooms with a search space of 10^552.
18talks-6timeslots-5rooms has 18 talks, 6 timeslots and 5 rooms with a search space of 10^26.
36talks-12timeslots-5rooms has 36 talks, 12 timeslots and 5 rooms with a search space of 10^64.
72talks-12timeslots-10rooms has 72 talks, 12 timeslots and 10 rooms with a search space of 10^149.
108talks-18timeslots-10rooms has 108 talks, 18 timeslots and 10 rooms with a search space of 10^243.
216talks-18timeslots-20rooms has 216 talks, 18 timeslots and 20 rooms with a search space of 10^552.31.17. Rock tour
Drive the rock bus from show to show, but schedule shows only on available days.
Hard constraints:
- Schedule every required show.
- Schedule as many shows as possible.
Medium constraints:
- Maximize revenue opportunity.
- Minimize driving time.
- Visit sooner than later.
Soft constraints:
- Avoid long driving times.
Problem size
47shows has 47 shows with a search space of 10^59.
47shows has 47 shows with a search space of 10^59.31.18. Flight crew scheduling
Assign flights to pilots and flight attendants.
Hard constraints:
- Required skill: each flight assignment has a required skill. For example, flight AB0001 requires 2 pilots and 3 flight attendants.
- Flight conflict: each employee can only attend one flight at the same time
- Transfer between two flights: between two flights, an employee must be able to transfer from the arrival airport to the departure airport. For example, Ann arrives in Brussels at 10:00 and departs in Amsterdam at 15:00.
- Employee unavailability: the employee must be available on the day of the flight. For example, Ann is on PTO on 1-Feb.
Soft constraints:
- First assignment departing from home
- Last assignment arriving at home
- Load balance flight duration total per employee
Problem size
175flights-7days-Europe has 2 skills, 50 airports, 150 employees, 175 flights and 875 flight assignments with a search space of 10^1904. 700flights-28days-Europe has 2 skills, 50 airports, 150 employees, 700 flights and 3500 flight assignments with a search space of 10^7616. 875flights-7days-Europe has 2 skills, 50 airports, 750 employees, 875 flights and 4375 flight assignments with a search space of 10^12578. 175flights-7days-US has 2 skills, 48 airports, 150 employees, 175 flights and 875 flight assignments with a search space of 10^1904.
175flights-7days-Europe has 2 skills, 50 airports, 150 employees, 175 flights and 875 flight assignments with a search space of 10^1904.
700flights-28days-Europe has 2 skills, 50 airports, 150 employees, 700 flights and 3500 flight assignments with a search space of 10^7616.
875flights-7days-Europe has 2 skills, 50 airports, 750 employees, 875 flights and 4375 flight assignments with a search space of 10^12578.
175flights-7days-US has 2 skills, 48 airports, 150 employees, 175 flights and 875 flight assignments with a search space of 10^1904.
'%20d='M201.5%20305.5c-13.8%200-24.9-11.1-24.9-24.6%200-13.8%2011.1-24.9%2024.9-24.9%2013.6%200%2024.6%2011.1%2024.6%2024.9%200%2013.6-11.1%2024.6-24.6%2024.6zM504%20256c0%20137-111%20248-248%20248S8%20393%208%20256%20119%208%20256%208s248%20111%20248%20248zm-132.3-41.2c-9.4%200-17.7%203.9-23.8%2010-22.4-15.5-52.6-25.5-86.1-26.6l17.4-78.3%2055.4%2012.5c0%2013.6%2011.1%2024.6%2024.6%2024.6%2013.8%200%2024.9-11.3%2024.9-24.9s-11.1-24.9-24.9-24.9c-9.7%200-18%205.8-22.1%2013.8l-61.2-13.6c-3-.8-6.1%201.4-6.9%204.4l-19.1%2086.4c-33.2%201.4-63.1%2011.3-85.5%2026.8-6.1-6.4-14.7-10.2-24.1-10.2-34.9%200-46.3%2046.9-14.4%2062.8-1.1%205-1.7%2010.2-1.7%2015.5%200%2052.6%2059.2%2095.2%20132%2095.2%2073.1%200%20132.3-42.6%20132.3-95.2%200-5.3-.6-10.8-1.9-15.8%2031.3-16%2019.8-62.5-14.9-62.5zM302.8%20331c-18.2%2018.2-76.1%2017.9-93.6%200-2.2-2.2-6.1-2.2-8.3%200-2.5%202.5-2.5%206.4%200%208.6%2022.8%2022.8%2087.3%2022.8%20110.2%200%202.5-2.2%202.5-6.1%200-8.6-2.2-2.2-6.1-2.2-8.3%200zm7.7-75c-13.6%200-24.6%2011.1-24.6%2024.9%200%2013.6%2011.1%2024.6%2024.6%2024.6%2013.8%200%2024.9-11.1%2024.9-24.6%200-13.8-11-24.9-24.9-24.9z'/%3e%3c/svg%3e){kind=small}