第8章 Exhaustive Search (しらみつぶし探索)
8.1. 概要
しらみつぶし探索は常に大域的最適を見つけ認識しますが、スケールは行わない (その小規模のデータセットを超えることはない) ため、大抵は役に立ちません。
8.2. Brute Force (力まかせ)
8.2.1. アルゴリズムの説明
力まかせアルゴリズムは、可能性のあるすべての解を作成して評価します。
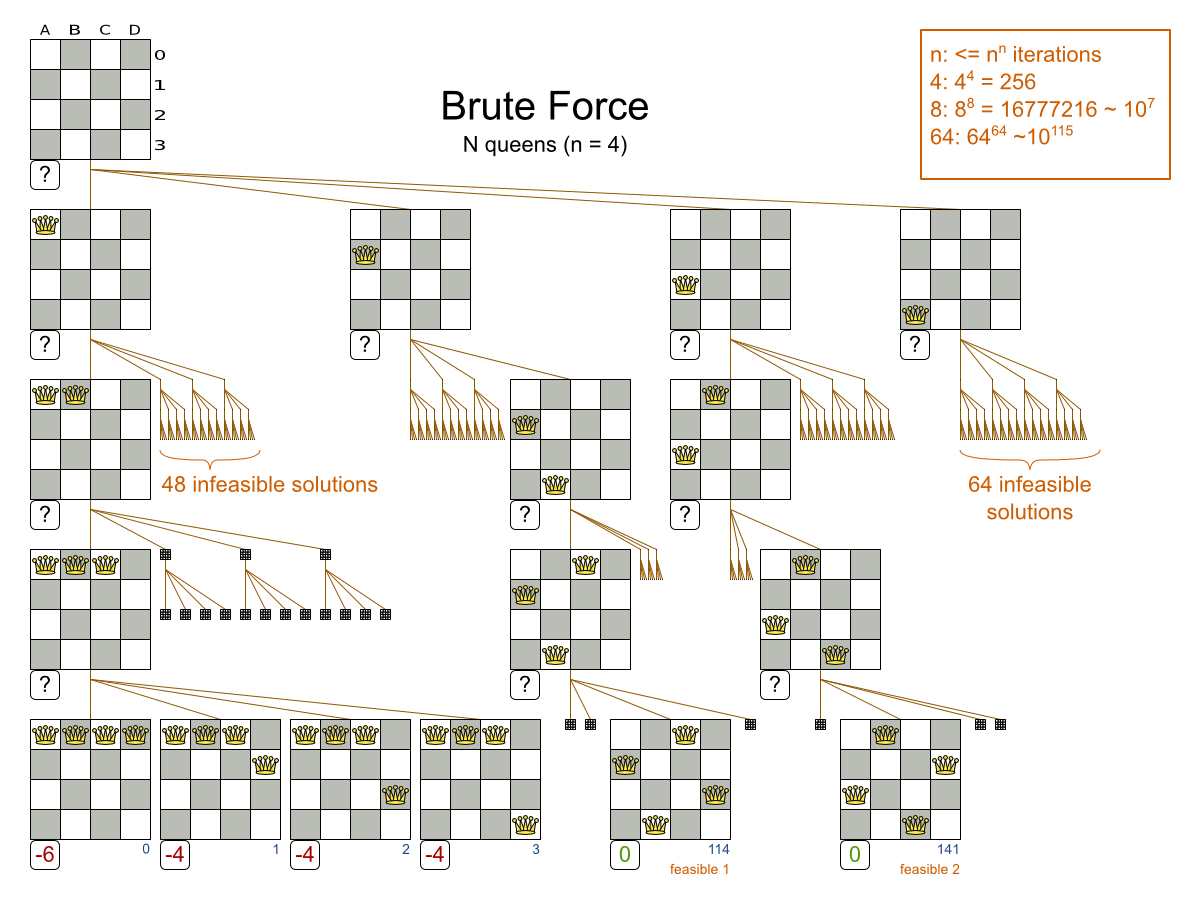
問題のサイズが大きくなると、探索ツリーが指数関数的に大きくなるため、スケーラビリティーの問題が発生します。
しらみつぶし探索のスケーラビリティー で説明しているように、力まかせは、通常、時間に制約のある現実社会で使用するには適しません。
8.2.2. 設定
力まかせの最も簡単な設定方法:
<solver>
...
<exhaustiveSearch>
<exhaustiveSearchType>BRUTE_FORCE</exhaustiveSearchType>
</exhaustiveSearch>
</solver>8.3. Branch And Bound (分枝限定)
8.3.1. アルゴリズムの説明
分岐限定も、指数関数的な探索木でノードを検証しますが、より見込みのあるノードを最初に調査して、見込みのないノードを取り除きます。
各ノードに対して、分岐限定は、最適な限界 (そのノードがつながる最適な可能スコア) を計算します。ノードの最適な限界が、グローバルの悲観的な限界と同じか、低くなる場合、そのノードは取り除かれます (その全サブノードの分岐全体を含む)。
学術論文では、楽観限界 (optimistic bound) の代わりに下界 (lower bound) という用語を使用し、悲観限界 (pessimistic bound) の代わりに上界 (upper bound) という用語を使用します。これは、スコアを最小限に抑えるためです。
Planner は、(否定または肯定の制約を組み合わせて対応するため) スコアを最大限に活用します。したがって、それを明確にするために異なる用語を使用します。常に高い限界なのに下限という用語を使用すると紛らわしくなるためです。
たとえば、インデックス 14 で、グローバルの楽観限界を -2 に設定します。インデックス 11 にたどり着いたノードから到達できるすべての解が、-2 (ノードの楽観限界)と同じか、低くなるため、その解は除外できます。
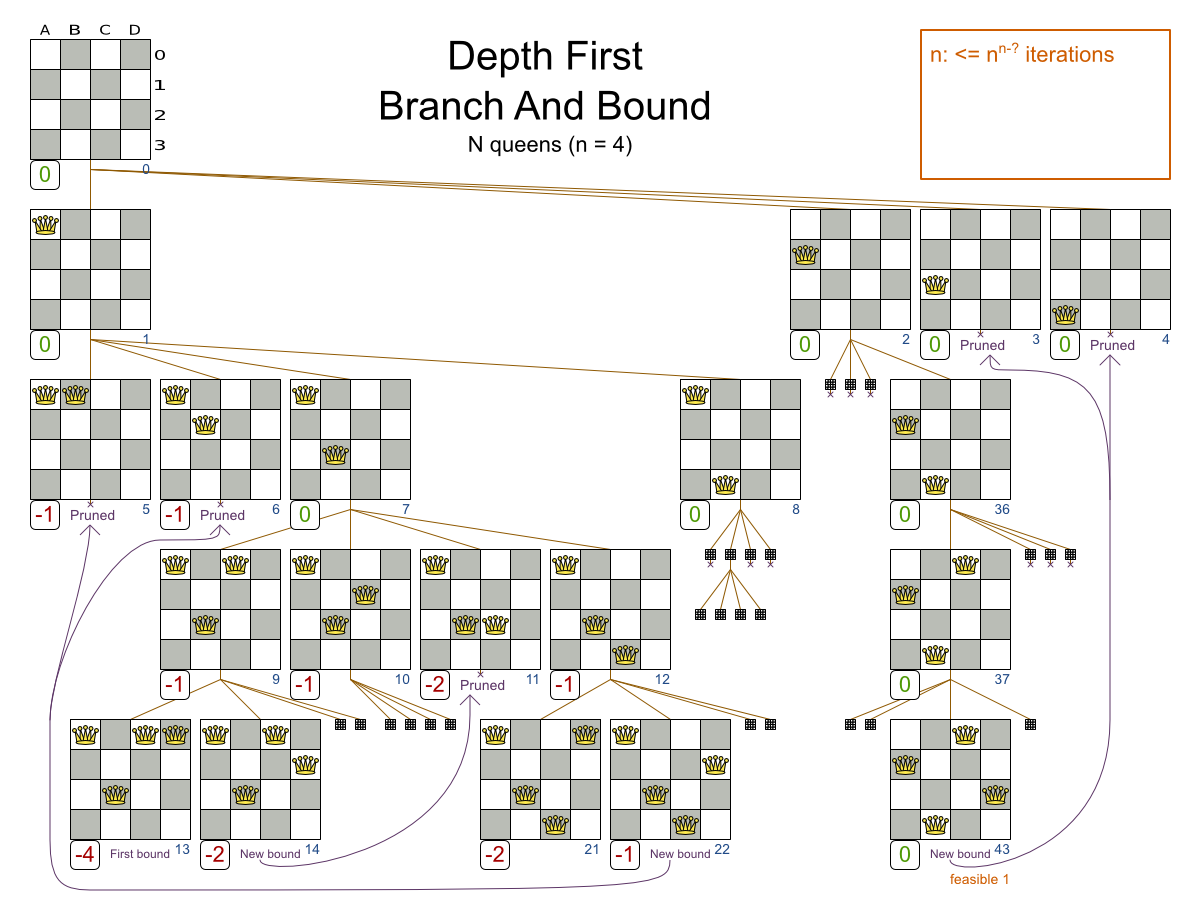
(力まかせ とほぼ同じく) 分岐限定は、問題のサイズが大きくなると指数関数的に大きくなる探索木を作成します。したがって、少し遅れるだけで、結局は同じスケーラビリティーの壁に到達します。
分岐限定は、時間が限られているため、通常は、しらみつぶし探索のスケーラビリティー で説明しているように、現実の問題に対してはほぼ使用できません。
8.3.2. 設定
分枝限定の最も簡単な設定:
<solver>
...
<exhaustiveSearch>
<exhaustiveSearchType>BRANCH_AND_BOUND</exhaustiveSearchType>
</exhaustiveSearch>
</solver>
枝刈りが、デフォルトの ScoreBounder と連携するには、InitializingScoreTrend を設定する必要があります。特に、ONLY_DOWN の InitializingScoreTrend (または最高スコアレベルに ONLY_DOWN がある) が、多くを除外します。
高度な設定方法:
<exhaustiveSearch>
<exhaustiveSearchType>BRANCH_AND_BOUND</exhaustiveSearchType>
<nodeExplorationType>DEPTH_FIRST</nodeExplorationType>
<entitySorterManner>DECREASING_DIFFICULTY_IF_AVAILABLE</entitySorterManner>
<valueSorterManner>INCREASING_STRENGTH_IF_AVAILABLE</valueSorterManner>
</exhaustiveSearch>
nodeExplorationType オプション:
DEPTH_FIRST(デフォルト): より深いノードを最初に調べます (そしてスコアが良いもの、より楽観的な限界の順)。より深いノード (特に葉節点) は悲観限界だけを改善します。悲観限界を向上させると、ノードがさらに除外されるため、探索領域が減ります。<exhaustiveSearch> <exhaustiveSearchType>BRANCH_AND_BOUND</exhaustiveSearchType> <nodeExplorationType>DEPTH_FIRST</nodeExplorationType> </exhaustiveSearch>BREADTH_FIRST(推奨されません): 1 レイヤーずつ (次にスコアが良いもの、楽観限界が良いものの順に)、ノードを調べます。メモリーで (そして通常はパフォーマンスでも) 大きくスケールします。<exhaustiveSearch> <exhaustiveSearchType>BRANCH_AND_BOUND</exhaustiveSearchType> <nodeExplorationType>BREADTH_FIRST</nodeExplorationType> </exhaustiveSearch>SCORE_FIRST: スコアが高いノードを最初に調べます (そして、より楽観的な限界、ノードが深いものの順に)。場合によっては、BREADTH_FIRSTと同じだけスケールします。<exhaustiveSearch> <exhaustiveSearchType>BRANCH_AND_BOUND</exhaustiveSearchType> <nodeExplorationType>SCORE_FIRST</nodeExplorationType> </exhaustiveSearch>OPTIMISTIC_BOUND_FIRST: 楽観的限界が良いノードを最初に調べます (そして、スコアが良いもの、ノードが深いものの順)。場合によっては、BREADTH_FIRSTと同じだけスケールします。<exhaustiveSearch> <exhaustiveSearchType>BRANCH_AND_BOUND</exhaustiveSearchType> <nodeExplorationType>OPTIMISTIC_BOUND_FIRST</nodeExplorationType> </exhaustiveSearch>
entitySorterManner オプションは、以下のようになります。
-
DECREASING_DIFFICULTY: 難しいプランニングエンティティーが最初に初期化されます。これにより、通常は、枝刈りが改善 (したがってスケーラビリティーが改善) します。モデルが プランニングエンティティーの難易度比較 に対応している必要があります。 -
DECREASING_DIFFICULTY_IF_AVAILABLE(デフォルト): モデルが プランニングエンティティーの難易度比較 に対応してる場合はDECREASING_DIFFICULTYと同じ動作になり、対応していない場合はNONEと同じになります。 -
NONE: 元の順番で、プランニングエンティティーを初期化します。
valueSorterManner オプションは、以下のようになります。
-
INCREASING_STRENGTH: 計画値の強度が小さいものから順に評価します。モデルが 計画値の強度比較 に対応している必要があります。 -
INCREASING_STRENGTH_IF_AVAILABLE(デフォルト): モデルが 計画値の強度比較 に対応している場合はINCREASING_STRENGTHと同じ動作になり、対応していない場合はNONEと同じになります。 -
DECREASING_STRENGTH: 計画値の強度が大きいものから順に評価します。モデルが 計画値の強度比較 に対応している必要があります。 -
DECREASING_STRENGTH_IF_AVAILABLE: モデルが 計画値の強度比較 に対応している場合はDECREASING_STRENGTHと同じ動作になります。対応していない場合はNONEと同じになります。 -
NONE: 元の順番で、計画値を試します。
8.4. しらみつぶし探索のスケーラビリティー
各種しらみつぶし探索には、以下のような重要なスケーラビリティー問題があります。
- メモリー使用のスケーラビリティーが極めて低い。
- パフォーマンスのスケーラビリティーが極めて低い。
ベンチマーカー における、時間経過のグラフで示されるように、力まかせ (Brute Force) と分岐限定 (Branch And Bound) の両方に、パフォーマンスのスケーラビリティーの壁が立ちはだかります。たとえば、N クィーンでは、クィーンの数が数十になれば行き詰まります。
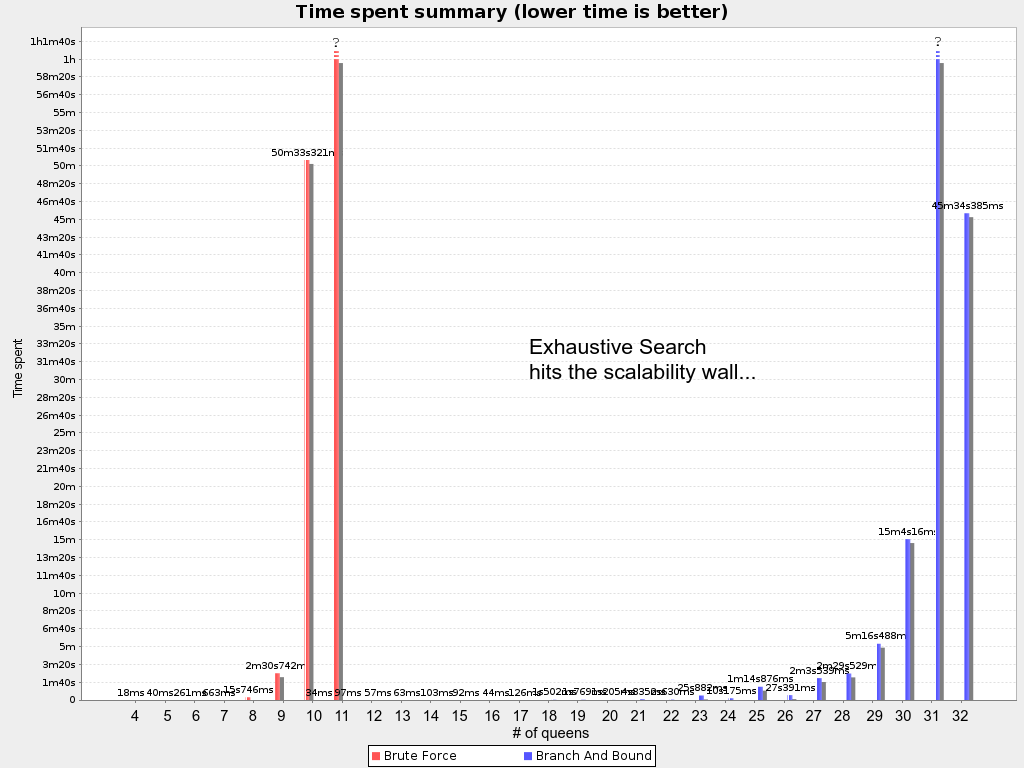
クラウドのバランスなどの多くのユースケースでは、壁が突然出現します。
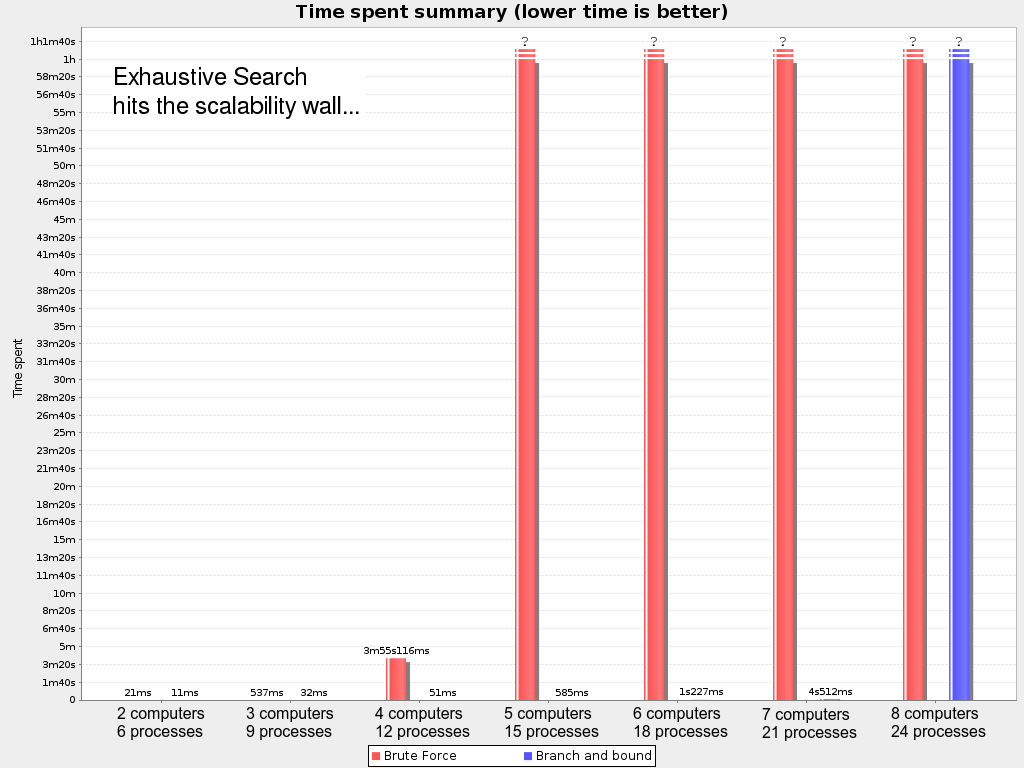
しらみつぶし探索は、データセットが小さい場合でもすでにこの壁があります。したがって、本番環境では、この最適化アルゴリズムはほとんど役に立ちません。代わりに構築ヒューリスティックと局所探索法を組み合わせ使用します。これにより、クイーンやコンピューターの数が数千になっても、簡単に処理できます。
このスケーラビリティー問題について、ハードウェアでは目立った影響はありません。新しいハードウェアが出現しても、大海の中のひとしずくとなります。ムーアの法則ですら、データセットにさらにいくつかのプランニングエンティティーが発生すれば勝てません。
