第3章 ユースケースおよびサンプル
3.1. サンプルの概要
Planner にはサンプルが複数含まれます。本書では、N クィーンの例とクラウドのバランスの例を主に使用するため、少なくてもこの 2 つのセクションは目を通しておいてください。
サンプルのソースコードは、examples/sources に保存されているディストリビューション ZIP か、optaplanner/optaplanner-examples の git から入手できます。
| 例 | ドメイン | サイズ | コンペティションの有無 | 使用する特別機能 |
|---|---|---|---|---|
|
|
|
なし | |
|
|
| ||
|
|
| ||
|
|
|
| |
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
|
| ||
|
時間枠がある中での 配送経路 |
配送経路に関する追加機能:
|
|
|
配送経路に関する追加機能:
|
|
|
| ||
|
|
| ||
|
|
|
| |
|
|
| ||
|
|
|
| |
|
|
| ||
|
|
|
現実的なコンペティション とは、以下のような公式で独立したコンペティションを指します。
- 実際のユースケースを明確に定義するコンペティション
- 実際の制約があるコンペティション
- 実際のデータセットが複数あるコンペティション
- 特定のハードウェアで特定の時間内に結果を再現できるコンペティション
- 教育機関および/または企業の運用研究コミュニティーが真剣に参加しているコンペティション
このような現実的なコンペティションでは、Planner を、競合のソフトウェアや教育研究と客観的に比較することができます。
3.2. 基本例
3.2.1. N クィーン
3.2.1.1. 問題の詳細
n サイズのチェスボードで、他のクィーンに取られない位置に n 個のクィーンを置きます。最も一般的なクィーンパズルは、n = 8 の 8 個のクィーンパズルです。
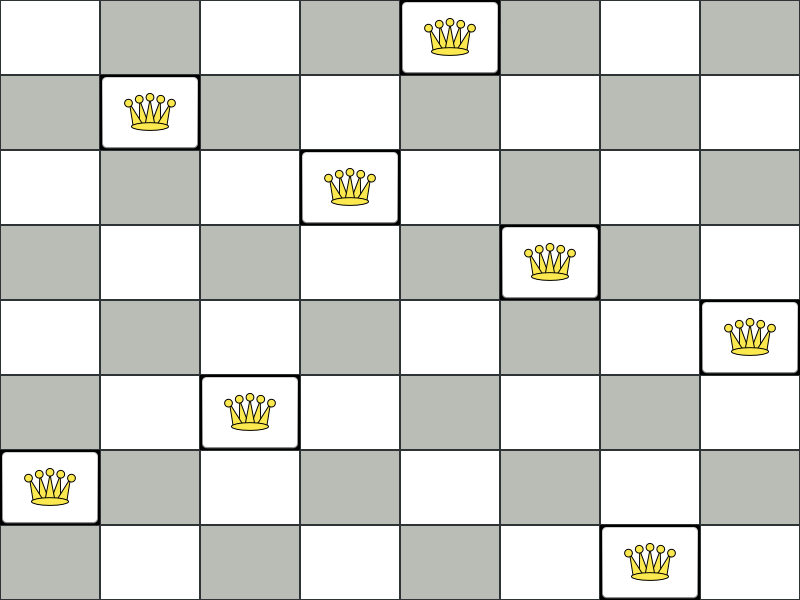
制約:
- n 行および n 列のチェスボードを使用します。
- チェスボードに n 個のクィーンを置きます。
- クィーンが他のクィーンに取られないように配置します。クィーンは、同じ水平線上、垂直線上、対角線上にある他のクィーンを取ることができます。
本書の例では、クィーン 4 個のパズルを主に使用します。
以下が提案された解です。
図3.1 クィーン 4 個のパズルの誤った解
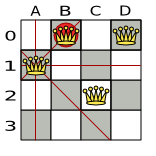
上記の解は、A1 と B0 (および B0 と D0) のクィーンがお互いに駒を取れるので間違っています。B0 のクィーンをどかせば「他のクィーンに取られないようにする」という制約は順守できますが、「n 個のクィーンを置く」という制約に違反します。
以下は正しい解です。
図3.2 クィーン 4 個のパズルの正しい解
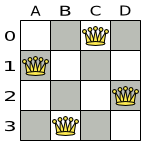
すべての制約が満たされているので、これが正解です。n クィーンパズルでは、正解が複数存在する場合が多々あります。各 n に対して、考えられるすべての解を見つけるのではなく、正しい解を 1 つ導き出すことにフォーカスします。
3.2.1.2. 問題の規模
4queens has 4 queens with a search space of 256. 8queens has 8 queens with a search space of 10^7. 16queens has 16 queens with a search space of 10^19. 32queens has 32 queens with a search space of 10^48. 64queens has 64 queens with a search space of 10^115. 256queens has 256 queens with a search space of 10^616.
N クィーンは、初心者用のサンプルとして実装されているため、最適化はされていませんが、クィーンが 64 個になっても簡単に処理できます。何点か変更を加えると、クィーンが 5000 個以上になっても簡単に対応できることが立証されています。
3.2.1.3. ドメインモデル
適切なドメインモデルを使用してください。計画の問題の理解と解決がより簡単になります。以下は、n クィーン問題を例にドメインモデルを使用したものです。
public class Column {
private int index;
// ... getters and setters
}public class Row {
private int index;
// ... getters and setters
}public class Queen {
private Column column;
private Row row;
public int getAscendingDiagonalIndex() {...}
public int getDescendingDiagonalIndex() {...}
// ... getters and setters
}
Queen インスタンスには Column (例: 0 は列 A、1 は列 B) および Row (例: 0 は行 0、1 は行 1) が含まれます。列と行をもとに、昇順の対角線、降順の対角線を計算することができます。列と行のインデックスは、チェスボードの左上隅から数えています。
public class NQueens implements Solution<SimpleScore> {
private int n;
private List<Column> columnList;
private List<Row> rowList;
private List<Queen> queenList;
private SimpleScore score;
// ... getters and setters
}
1 つの NQueens インスタンスには Queen インスタンスの一覧が含まれています。これが Solution 実装として提供され、Solver が解決して読み出します。たとえば、4 クイーンの例では、NQueens の getN() メソッドが常に 4 を返します。
| 解 | クィーン | columnIndex | rowIndex | ascendingDiagonalIndex (columnIndex + rowIndex) | descendingDiagonalIndex (columnIndex - rowIndex) |
|---|---|---|---|---|---|
|
A1 |
0 |
1 |
1 (**) |
-1 |
|
B0 |
1 |
0 (*) |
1 (**) |
1 | |
|
C2 |
2 |
2 |
4 |
0 | |
|
D0 |
3 |
0 (*) |
3 |
3 |
(*) や (**) のように、クィーン 2 つが同じ行、列、対角線を共有する場合は、2 つの駒が互いを取ることができます。
3.2.2. クラウドのバランス
この例は、チュートリアル で説明されています。
3.2.3. 巡回セールスマン (TSP - 巡回セールスマン問題)
3.2.3.1. 問題の詳細
都市の一覧をもとに、セールスマンが最短距離で、各都市を 1 度だけ訪問するルートを探します。
この問題は ウィキペディア に定義されています。これは、計算数学で 最も熱心に研究された問題の 1 つです。大概は、従業員のシフト勤務など、その他の制約と一緒に計画の問題の一部として使用されます。
3.2.3.2. 問題の規模
dj38 has 38 cities with a search space of 10^58. europe40 has 40 cities with a search space of 10^62. st70 has 70 cities with a search space of 10^126. pcb442 has 442 cities with a search space of 10^1166. lu980 has 980 cities with a search space of 10^2927.
3.2.3.3. 問題の難易度
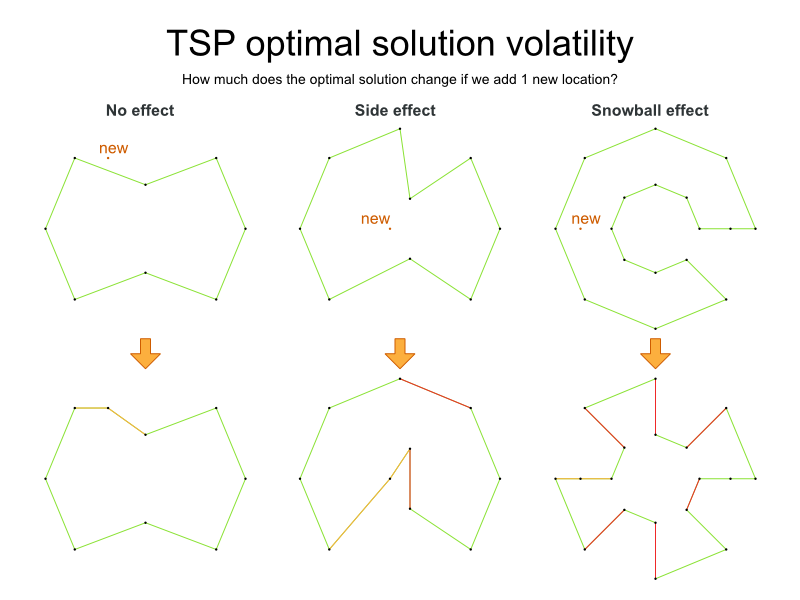
TSP の定義は単純ですが、問題の解決は驚くほど難しくなります。これは NP 困難問題と呼ばれ、多くの計画の問題と同様、特定の問題のデータセットに対する最適な解は、その問題のデータセットが少しでも変更すると、大幅に変化する可能性があります。
3.2.4. ディナーパーティー
3.2.4.1. 問題の詳細
マナーズさんがディナーパーティを再度開催することにしました。
- 今回は、ゲスト 144 名を招待し、円卓を 12 個用意し、各テーブルに椅子を 12 席用意しました。
- 座席は、同じ性別の人が隣同士にならないようにします。
- また、隣の人とは必ず、同じ趣味を 1 つ持つようにします。
- 各テーブルには、政治家、医者、著名人、コーチ、教師、そしてプログラマーを 2 名ずつ配置します。
- 政治家、医者、コーチ、プログラマーは、それぞれ同じ業種の人が同じテーブルにならないようにします。
Drools Expert にも、(サイズがはるかに小さい) 一般的なミスマナーズの例が含まれており、包括的なヒューリスティックを採用して解を導き出しています。Planner の実装は、ヒューリスティックを使用して最適解を見つけ、Drools Expert を使用して各解のスコアを計算するため、スケーラビリティーがはるかに高くなっています。
3.2.4.2. 問題の規模
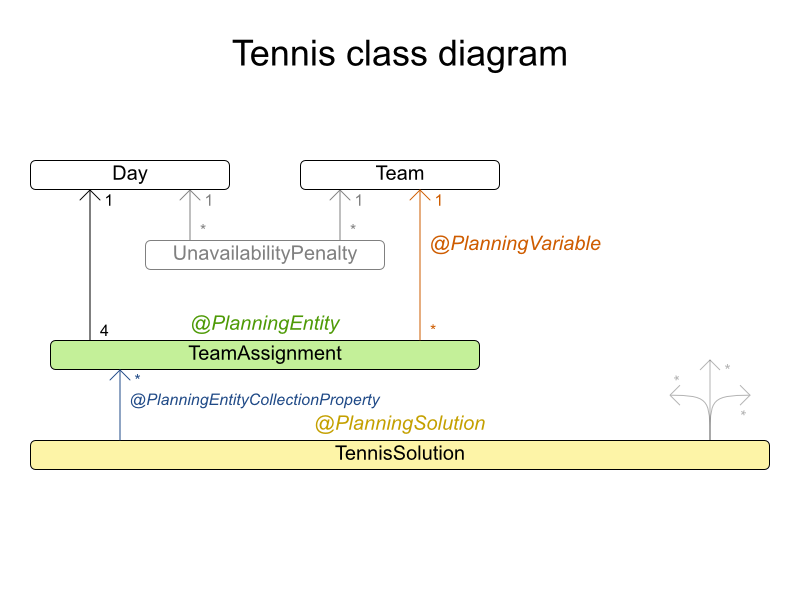
wedding01 has 18 jobs, 144 guests, 288 hobby practicians, 12 tables and 144 seats with a search space of 10^310.
3.2.5. テニスクラブのスケジュール
3.2.5.1. 問題の詳細
テニスクラブでは、毎週 4 チームが総あたりで試合をします。4 つの対戦枠を公平にチームに割り当てます。
ハード制約:
- 制約: チームは 1 日に 1 回だけ試合ができる。
- 参加不可: 日程によって参加できないチームがある。
中程度の制約:
- 公平な割り当て: 各チームが試合をする回数を (ほぼ) 同じにする。
ソフト制約:
- 均等に対戦: 各チームが、各対戦相手と対戦する回数を同じにする。
3.2.5.2. 問題の規模
munich-7teams has 7 teams, 18 days, 12 unavailabilityPenalties and 72 teamAssignments with a search space of 10^60.
3.2.5.3. ドメインモデル
3.2.6. 会議のスケジュール
3.2.6.1. 問題の詳細
各会議に、開始時間と会議室を割り当てます。会議の長さは異なります。
ハード制約:
- 部屋の制約: 2 つの会議が、同じ時間に同じ会議室を使用することはできない。
- 必須の出席者: 同じ時間に開催される必須の会議を 2 つ割り当てることはできない。
中程度の制約:
- 任意の出席者: 同じ時間に開催される任意の会議を 2 つ割り当てることはできない。また、任意の会議、および必須の会議をそれぞれ 1 つ割り当てることはできない。
ソフト制約:
- 早い段階でスケジュール: すべての会議をできるだけ早くスケジュールする。
3.2.6.2. 問題の規模
50meetings-160timegrains-5rooms has 50 meetings, 160 timeGrains and 5 rooms with a search space of 10^145. 100meetings-320timegrains-5rooms has 100 meetings, 320 timeGrains and 5 rooms with a search space of 10^320.
3.3. 実例
3.3.1. コースの時間割 (ITC 2007 Track 3 - カリキュラムのスケジュール)
3.3.1.1. 問題の詳細
各授業を、時間枠および講義室に割り当ててスケジュールを組みます。
ハード制約:
- 講師の制約: 各講師は、同じ時間に授業を 2 つ受け持つことはできない。
- カリキュラムの制約: 1 つのカリキュラムに、2 つの授業を同じ時間に設定することはできない。
- 部屋の占有: 同じ時間 (Period) の同じ講義室に、2 つの授業を割り当てることはできない。
- 利用不可の時間 (データセットごとに指定): 授業には割り当てられない時間がある。
ソフト制約:
- 講義室の収容人数: 講義室の収容人数は、その授業を受ける学生の数よりも多くなければならない。
- 最小限の就業日数: 同じコースの授業の開講期間は、最短になるようにする。
- カリキュラムの緊密さ: 同じカリキュラムに含まれる授業は、時間帯を近く (連続した時間に) 設定する。
- 講義室の不変性: 同じコースの授業は同じ講義室を割り当てる必要がある。
この問題は International Timetabling Competition 2007 track 3 で定義されています。
3.3.1.2. 問題の規模
comp01 has 24 teachers, 14 curricula, 30 courses, 160 lectures, 30 periods, 6 rooms and 53 unavailable period constraints with a search space of 10^360. comp02 has 71 teachers, 70 curricula, 82 courses, 283 lectures, 25 periods, 16 rooms and 513 unavailable period constraints with a search space of 10^736. comp03 has 61 teachers, 68 curricula, 72 courses, 251 lectures, 25 periods, 16 rooms and 382 unavailable period constraints with a search space of 10^653. comp04 has 70 teachers, 57 curricula, 79 courses, 286 lectures, 25 periods, 18 rooms and 396 unavailable period constraints with a search space of 10^758. comp05 has 47 teachers, 139 curricula, 54 courses, 152 lectures, 36 periods, 9 rooms and 771 unavailable period constraints with a search space of 10^381. comp06 has 87 teachers, 70 curricula, 108 courses, 361 lectures, 25 periods, 18 rooms and 632 unavailable period constraints with a search space of 10^957. comp07 has 99 teachers, 77 curricula, 131 courses, 434 lectures, 25 periods, 20 rooms and 667 unavailable period constraints with a search space of 10^1171. comp08 has 76 teachers, 61 curricula, 86 courses, 324 lectures, 25 periods, 18 rooms and 478 unavailable period constraints with a search space of 10^859. comp09 has 68 teachers, 75 curricula, 76 courses, 279 lectures, 25 periods, 18 rooms and 405 unavailable period constraints with a search space of 10^740. comp10 has 88 teachers, 67 curricula, 115 courses, 370 lectures, 25 periods, 18 rooms and 694 unavailable period constraints with a search space of 10^981. comp11 has 24 teachers, 13 curricula, 30 courses, 162 lectures, 45 periods, 5 rooms and 94 unavailable period constraints with a search space of 10^381. comp12 has 74 teachers, 150 curricula, 88 courses, 218 lectures, 36 periods, 11 rooms and 1368 unavailable period constraints with a search space of 10^566. comp13 has 77 teachers, 66 curricula, 82 courses, 308 lectures, 25 periods, 19 rooms and 468 unavailable period constraints with a search space of 10^824. comp14 has 68 teachers, 60 curricula, 85 courses, 275 lectures, 25 periods, 17 rooms and 486 unavailable period constraints with a search space of 10^722.
3.3.1.3. ドメインモデル
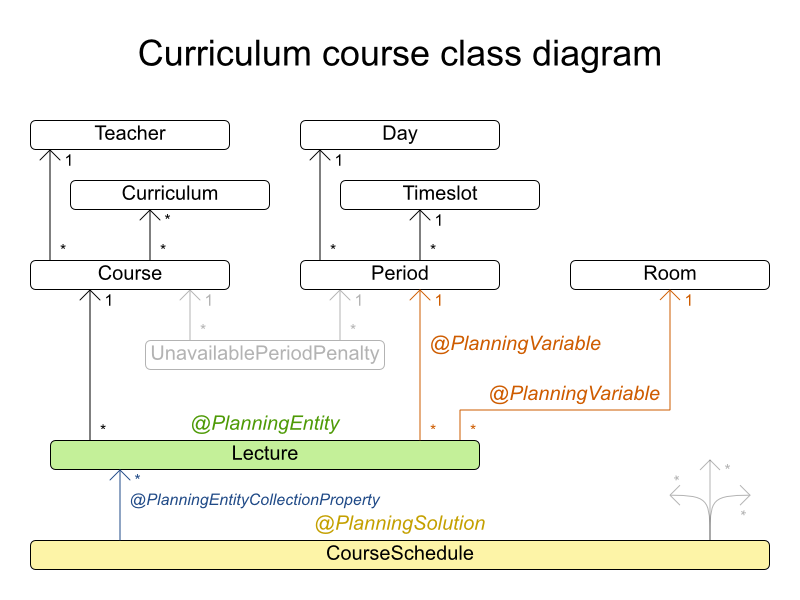
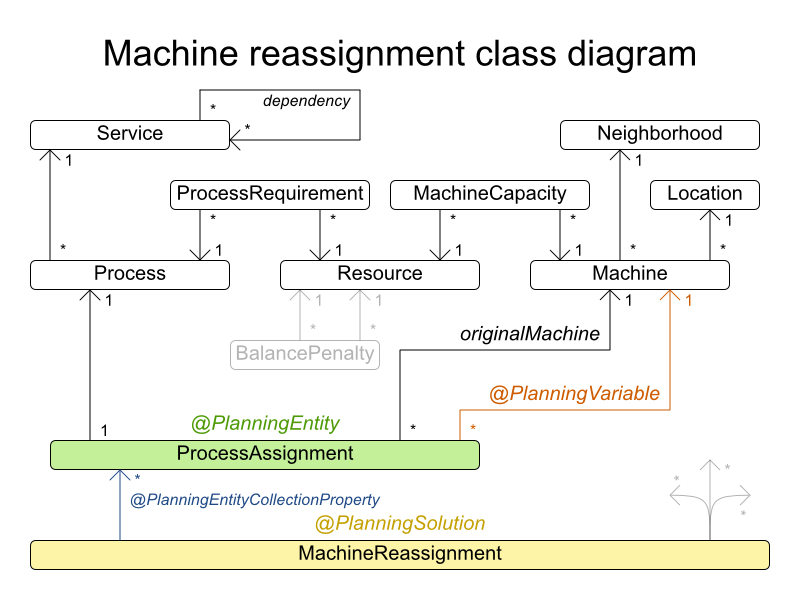
3.3.2. マシンの再割当て (Google ROADEF 2012)
3.3.2.1. 問題の詳細
各プロセスをマシンに割り当てます。全プロセスには、すでに元の (最適化されていない) 割り当てがあります。プロセスにはそれぞれ、各リソース (CPU、メモリーなど) が一定量必要です。これは、クラウドのバランスの例の応用です。
ハード制約:
- 最大容量: マシンに割り当てる各リソースはこの量を超えてはいけない。
- 制約: 同じサービスのプロセスは別のマシンで実行する必要がある。
- 分散: 同じサービスのプロセスは複数の場所に分散させる必要がある。
- 依存関係: 他のサービスに依存するサービスのプロセスは、そのサービスの近くで実行する必要がある。
- 一時的な使用: リソースによっては一時的なものがあり、元のマシンと、新たに割り当てられたマシンの両方の最大容量にカウントされる。
ソフト制約:
- 負荷: 各マシンの各リソースの安全容量を超えてはいけない。
- 負荷分散: 各マシンで利用可能なリソースを分散させて、今後の割り当てに対応できるように容量を空ける。
- プロセスの移動コスト: プロセスには移動コストが発生する。
- サービスの移動コスト: サービスには移動コストが発生する。
- 機械の移動コスト: マシン A からマシン B にプロセスを移動すると、A から B に固有の移動コストが別途発生する。
この問題は the Google ROADEF/EURO Challenge 2012 で定義されています。
3.3.2.2. 問題の規模
model_a1_1 has 2 resources, 1 neighborhoods, 4 locations, 4 machines, 79 services, 100 processes and 1 balancePenalties with a search space of 10^60. model_a1_2 has 4 resources, 2 neighborhoods, 4 locations, 100 machines, 980 services, 1000 processes and 0 balancePenalties with a search space of 10^2000. model_a1_3 has 3 resources, 5 neighborhoods, 25 locations, 100 machines, 216 services, 1000 processes and 0 balancePenalties with a search space of 10^2000. model_a1_4 has 3 resources, 50 neighborhoods, 50 locations, 50 machines, 142 services, 1000 processes and 1 balancePenalties with a search space of 10^1698. model_a1_5 has 4 resources, 2 neighborhoods, 4 locations, 12 machines, 981 services, 1000 processes and 1 balancePenalties with a search space of 10^1079. model_a2_1 has 3 resources, 1 neighborhoods, 1 locations, 100 machines, 1000 services, 1000 processes and 0 balancePenalties with a search space of 10^2000. model_a2_2 has 12 resources, 5 neighborhoods, 25 locations, 100 machines, 170 services, 1000 processes and 0 balancePenalties with a search space of 10^2000. model_a2_3 has 12 resources, 5 neighborhoods, 25 locations, 100 machines, 129 services, 1000 processes and 0 balancePenalties with a search space of 10^2000. model_a2_4 has 12 resources, 5 neighborhoods, 25 locations, 50 machines, 180 services, 1000 processes and 1 balancePenalties with a search space of 10^1698. model_a2_5 has 12 resources, 5 neighborhoods, 25 locations, 50 machines, 153 services, 1000 processes and 0 balancePenalties with a search space of 10^1698. model_b_1 has 12 resources, 5 neighborhoods, 10 locations, 100 machines, 2512 services, 5000 processes and 0 balancePenalties with a search space of 10^10000. model_b_2 has 12 resources, 5 neighborhoods, 10 locations, 100 machines, 2462 services, 5000 processes and 1 balancePenalties with a search space of 10^10000. model_b_3 has 6 resources, 5 neighborhoods, 10 locations, 100 machines, 15025 services, 20000 processes and 0 balancePenalties with a search space of 10^40000. model_b_4 has 6 resources, 5 neighborhoods, 50 locations, 500 machines, 1732 services, 20000 processes and 1 balancePenalties with a search space of 10^53979. model_b_5 has 6 resources, 5 neighborhoods, 10 locations, 100 machines, 35082 services, 40000 processes and 0 balancePenalties with a search space of 10^80000. model_b_6 has 6 resources, 5 neighborhoods, 50 locations, 200 machines, 14680 services, 40000 processes and 1 balancePenalties with a search space of 10^92041. model_b_7 has 6 resources, 5 neighborhoods, 50 locations, 4000 machines, 15050 services, 40000 processes and 1 balancePenalties with a search space of 10^144082. model_b_8 has 3 resources, 5 neighborhoods, 10 locations, 100 machines, 45030 services, 50000 processes and 0 balancePenalties with a search space of 10^100000. model_b_9 has 3 resources, 5 neighborhoods, 100 locations, 1000 machines, 4609 services, 50000 processes and 1 balancePenalties with a search space of 10^150000. model_b_10 has 3 resources, 5 neighborhoods, 100 locations, 5000 machines, 4896 services, 50000 processes and 1 balancePenalties with a search space of 10^184948.
3.3.2.3. ドメインモデル
3.3.3. 配送経路
3.3.3.1. 問題の詳細
複数の車両を使用して、各顧客の品物を回収し、倉庫まで運びます。1 つの車両で複数の顧客から品物を回収することはできますが、収容できる容量には限りがあります。
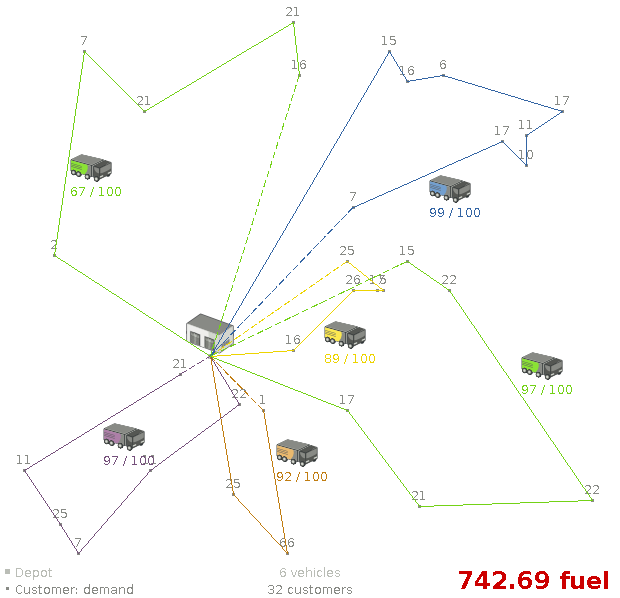
基本例 (CVRP) のほかに、時間枠の設定が加わった例 (CVRPTW) もあります。
ハード制約:
- 車両の容量: 車両は、車載容量を超えて品物を運ぶことができない。
時間枠 (CVRPTW のみ):
- 移動時間: 別の場所に移動する場合には時間がかかる。
- 顧客対応の時間: 車両は顧客に対応している時間、顧客先にとどまる必要がある。
- 顧客の準備が整う時間: 顧客の準備が整う前に車両が到着する可能性があるが、準備ができるまで待機してから顧客に対応する必要がある。
- 顧客が設定した締め切り時間: 車両は、顧客が設定した締め切り時間までに到着する必要がある。
ソフト制約:
- 合計距離: 車両が移動する合計距離 (ガソリンの消費量) を最小限に抑える。
CVRP (Capacitated Vehicle Routing Problem) と CVRPTW (Capacitated Vehicle Routing Problem with Time Window) は、VRP web で定義されています。
3.3.3.2. 問題の規模
CVRP インスタンス (時間枠なし):
A-n32-k5 has 1 depots, 5 vehicles and 31 customers with a search space of 10^46. A-n33-k5 has 1 depots, 5 vehicles and 32 customers with a search space of 10^48. A-n33-k6 has 1 depots, 6 vehicles and 32 customers with a search space of 10^48. A-n34-k5 has 1 depots, 5 vehicles and 33 customers with a search space of 10^50. A-n36-k5 has 1 depots, 5 vehicles and 35 customers with a search space of 10^54. A-n37-k5 has 1 depots, 5 vehicles and 36 customers with a search space of 10^56. A-n37-k6 has 1 depots, 6 vehicles and 36 customers with a search space of 10^56. A-n38-k5 has 1 depots, 5 vehicles and 37 customers with a search space of 10^58. A-n39-k5 has 1 depots, 5 vehicles and 38 customers with a search space of 10^60. A-n39-k6 has 1 depots, 6 vehicles and 38 customers with a search space of 10^60. A-n44-k7 has 1 depots, 7 vehicles and 43 customers with a search space of 10^70. A-n45-k6 has 1 depots, 6 vehicles and 44 customers with a search space of 10^72. A-n45-k7 has 1 depots, 7 vehicles and 44 customers with a search space of 10^72. A-n46-k7 has 1 depots, 7 vehicles and 45 customers with a search space of 10^74. A-n48-k7 has 1 depots, 7 vehicles and 47 customers with a search space of 10^78. A-n53-k7 has 1 depots, 7 vehicles and 52 customers with a search space of 10^89. A-n54-k7 has 1 depots, 7 vehicles and 53 customers with a search space of 10^91. A-n55-k9 has 1 depots, 9 vehicles and 54 customers with a search space of 10^93. A-n60-k9 has 1 depots, 9 vehicles and 59 customers with a search space of 10^104. A-n61-k9 has 1 depots, 9 vehicles and 60 customers with a search space of 10^106. A-n62-k8 has 1 depots, 8 vehicles and 61 customers with a search space of 10^108. A-n63-k10 has 1 depots, 10 vehicles and 62 customers with a search space of 10^111. A-n63-k9 has 1 depots, 9 vehicles and 62 customers with a search space of 10^111. A-n64-k9 has 1 depots, 9 vehicles and 63 customers with a search space of 10^113. A-n65-k9 has 1 depots, 9 vehicles and 64 customers with a search space of 10^115. A-n69-k9 has 1 depots, 9 vehicles and 68 customers with a search space of 10^124. A-n80-k10 has 1 depots, 10 vehicles and 79 customers with a search space of 10^149. F-n135-k7 has 1 depots, 7 vehicles and 134 customers with a search space of 10^285. F-n45-k4 has 1 depots, 4 vehicles and 44 customers with a search space of 10^72. F-n72-k4 has 1 depots, 4 vehicles and 71 customers with a search space of 10^131.
CVRPTW インスタンス (時間枠あり):
Solomon_025_C101 has 1 depots, 25 vehicles and 25 customers with a search space of 10^34. Solomon_025_C201 has 1 depots, 25 vehicles and 25 customers with a search space of 10^34. Solomon_025_R101 has 1 depots, 25 vehicles and 25 customers with a search space of 10^34. Solomon_025_R201 has 1 depots, 25 vehicles and 25 customers with a search space of 10^34. Solomon_025_RC101 has 1 depots, 25 vehicles and 25 customers with a search space of 10^34. Solomon_025_RC201 has 1 depots, 25 vehicles and 25 customers with a search space of 10^34. Solomon_100_C101 has 1 depots, 25 vehicles and 100 customers with a search space of 10^200. Solomon_100_C201 has 1 depots, 25 vehicles and 100 customers with a search space of 10^200. Solomon_100_R101 has 1 depots, 25 vehicles and 100 customers with a search space of 10^200. Solomon_100_R201 has 1 depots, 25 vehicles and 100 customers with a search space of 10^200. Solomon_100_RC101 has 1 depots, 25 vehicles and 100 customers with a search space of 10^200. Solomon_100_RC201 has 1 depots, 25 vehicles and 100 customers with a search space of 10^200. Homberger_0200_C1_2_1 has 1 depots, 50 vehicles and 200 customers with a search space of 10^460. Homberger_0200_C2_2_1 has 1 depots, 50 vehicles and 200 customers with a search space of 10^460. Homberger_0200_R1_2_1 has 1 depots, 50 vehicles and 200 customers with a search space of 10^460. Homberger_0200_R2_2_1 has 1 depots, 50 vehicles and 200 customers with a search space of 10^460. Homberger_0200_RC1_2_1 has 1 depots, 50 vehicles and 200 customers with a search space of 10^460. Homberger_0200_RC2_2_1 has 1 depots, 50 vehicles and 200 customers with a search space of 10^460. Homberger_0400_C1_4_1 has 1 depots, 100 vehicles and 400 customers with a search space of 10^1040. Homberger_0400_C2_4_1 has 1 depots, 100 vehicles and 400 customers with a search space of 10^1040. Homberger_0400_R1_4_1 has 1 depots, 100 vehicles and 400 customers with a search space of 10^1040. Homberger_0400_R2_4_1 has 1 depots, 100 vehicles and 400 customers with a search space of 10^1040. Homberger_0400_RC1_4_1 has 1 depots, 100 vehicles and 400 customers with a search space of 10^1040. Homberger_0400_RC2_4_1 has 1 depots, 100 vehicles and 400 customers with a search space of 10^1040. Homberger_0600_C1_6_1 has 1 depots, 150 vehicles and 600 customers with a search space of 10^1666. Homberger_0600_C2_6_1 has 1 depots, 150 vehicles and 600 customers with a search space of 10^1666. Homberger_0600_R1_6_1 has 1 depots, 150 vehicles and 600 customers with a search space of 10^1666. Homberger_0600_R2_6_1 has 1 depots, 150 vehicles and 600 customers with a search space of 10^1666. Homberger_0600_RC1_6_1 has 1 depots, 150 vehicles and 600 customers with a search space of 10^1666. Homberger_0600_RC2_6_1 has 1 depots, 150 vehicles and 600 customers with a search space of 10^1666. Homberger_0800_C1_8_1 has 1 depots, 200 vehicles and 800 customers with a search space of 10^2322. Homberger_0800_C2_8_1 has 1 depots, 200 vehicles and 800 customers with a search space of 10^2322. Homberger_0800_R1_8_1 has 1 depots, 200 vehicles and 800 customers with a search space of 10^2322. Homberger_0800_R2_8_1 has 1 depots, 200 vehicles and 800 customers with a search space of 10^2322. Homberger_0800_RC1_8_1 has 1 depots, 200 vehicles and 800 customers with a search space of 10^2322. Homberger_0800_RC2_8_1 has 1 depots, 200 vehicles and 800 customers with a search space of 10^2322. Homberger_1000_C110_1 has 1 depots, 250 vehicles and 1000 customers with a search space of 10^3000. Homberger_1000_C210_1 has 1 depots, 250 vehicles and 1000 customers with a search space of 10^3000. Homberger_1000_R110_1 has 1 depots, 250 vehicles and 1000 customers with a search space of 10^3000. Homberger_1000_R210_1 has 1 depots, 250 vehicles and 1000 customers with a search space of 10^3000. Homberger_1000_RC110_1 has 1 depots, 250 vehicles and 1000 customers with a search space of 10^3000. Homberger_1000_RC210_1 has 1 depots, 250 vehicles and 1000 customers with a search space of 10^3000.
3.3.3.3. ドメインモデル
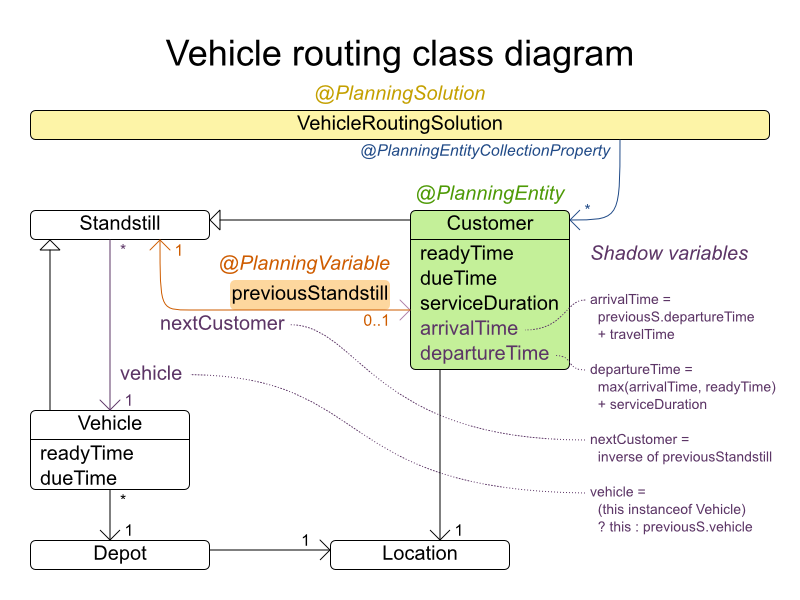
時間枠ありの配送経路のドメインモデルでは、シャドウ変数 を多用します。こうすることで、arrivalTime や departureTime などのプロパティーがドメインモデルで直接利用できるため、より自然に制約を表現することができます。
3.3.3.4. 直線距離ではなく道路の距離
車は、直線距離を移動するのではなく、道路や高速道路を使用する必要があります。ビジネスの観点からすると、これは非常に重要です。
最適化アルゴリズムでは、2 点の距離を検索できている (できれば、事前に計算されている) 場合には、これは特に重要ではありません。移動のコストについては、距離の代わりに移動時間、ガソリン代、またはこれらの重み関数をベースにすることも可能です。GraphHopper (埋め込み可能なオフライン Java エンジン)、Open MapQuest (web サービス)、Google Maps Client API (web サービス) など、移動コストを事前に計算する技術があります。
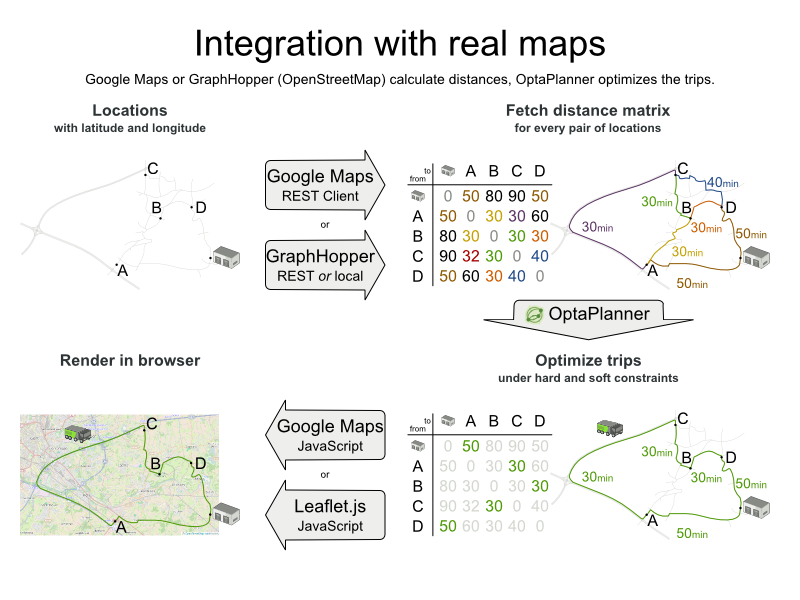
また、Leaflet や Google Maps for developers など、移動コストをレンダリングする技術もあります。optaplanner-webexamples-*.war には、このようなレンダリングのデモ例が含まれています。
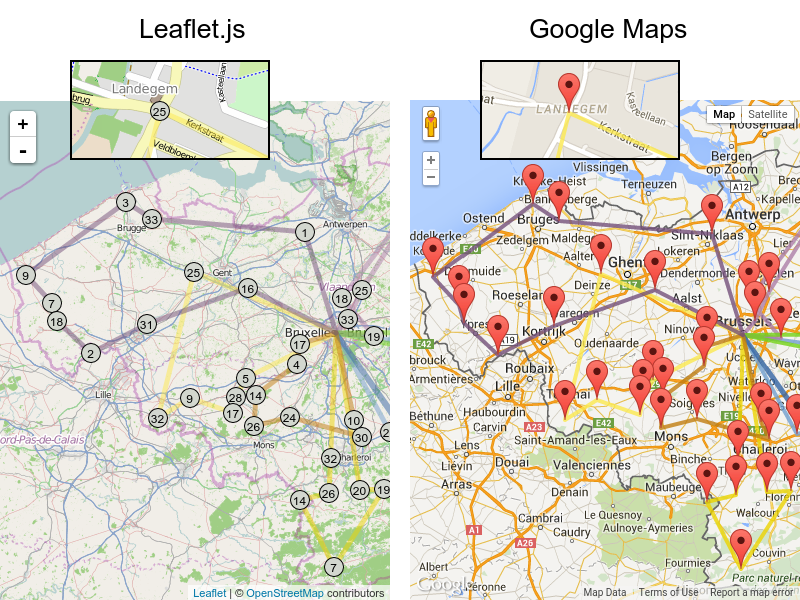
GraphHopper または Google Map Directions を使用して実際の経路をレンダリングすることも可能ですが、高速道路で経路が重なるため、停止する順番を確認するのが困難になります。
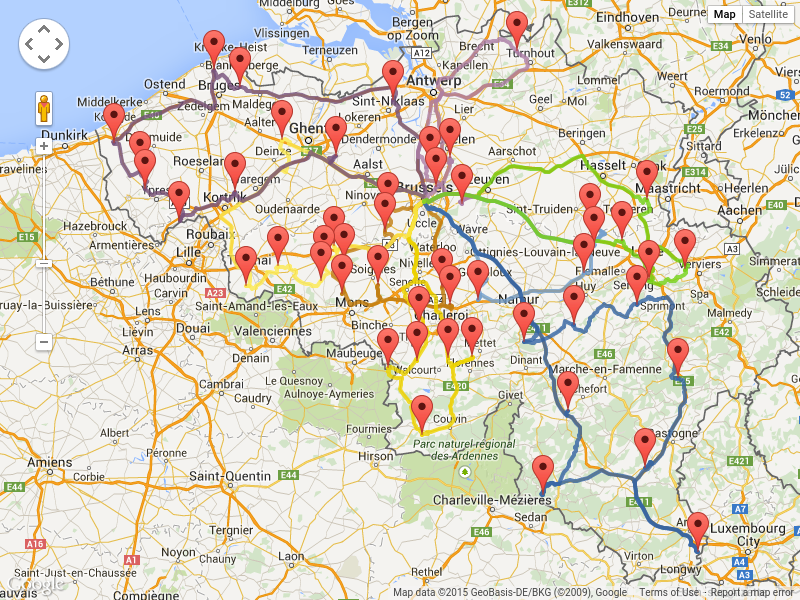
2 点間の移動コストは、Planner で使用したのと同じ最適化条件を使用する点に注意してください。たとえば、GraphHopper はデフォルトで、最短ではなく、最速の経路を返します。「最速」の GPS 経路の km (またはマイル) の距離を使用して、Planner で「最短」の移動を最適化しないようにしてください。以下のように、準最適な解が導き出される可能性があります。
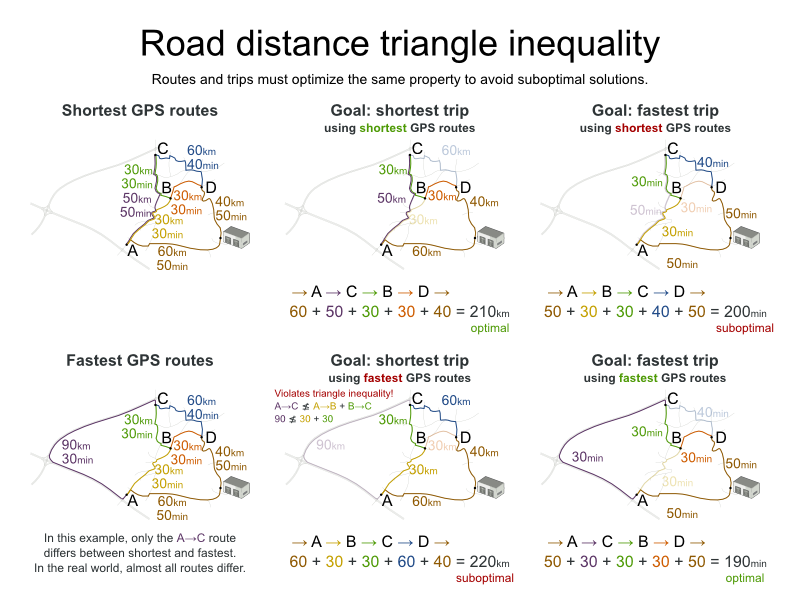
一般的な考え方とは異なり、多くのユーザーは最短の経路ではなく、最速の経路を使用したいと考えます。通常の道路よりも高速道路の使用を、舗装されていない道よりも舗装されている道路を好みます。実際には、最速の経路と、最短の経路が同じであることはほぼありません。
3.3.4. プロジェクトジョブのスケジュール
3.3.4.1. 問題の詳細
プロジェクトの遅延を最小限に抑えるために、すべてのジョブを時間内に実行できるようにスケジュールを設定します。各ジョブは、プロジェクトに含まれます。ジョブは、異なる方法で実行でき、方法ごとに期間や使用するリソースが異なります。これは、柔軟な ジョブショップスケジューリング (JSP) の応用です。
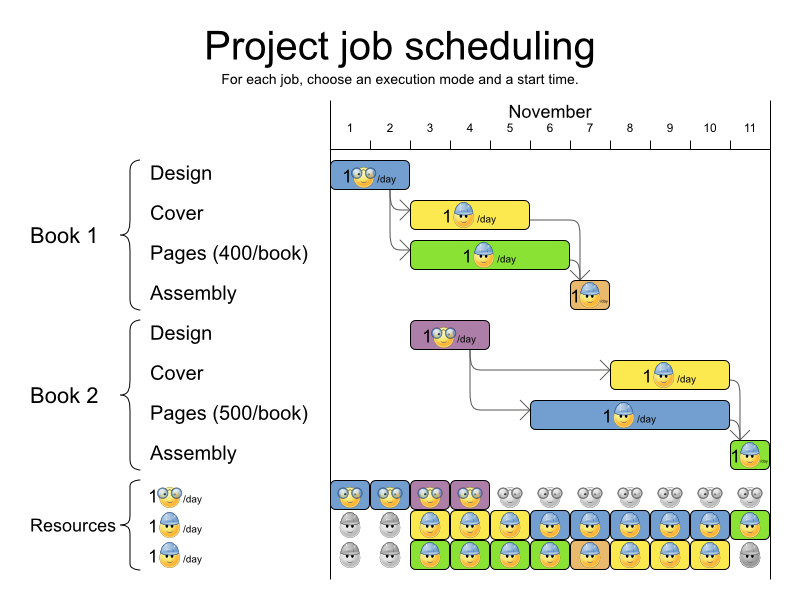
ハード制約:
- ジョブの優先順位: ジョブは、先行のジョブがすべて完了するまで開始しない。
リソースの容量: 利用可能な量を超えるリソースを使用しない。
- リソースはローカル (同じプロジェクトのジョブ間で共有)、またはグローバル (全ジョブ間で共有) とする。
- リソースは更新可能 (1 日に利用可能な容量) または更新不可 (全日で利用可能な容量) とする。
中程度の制約:
- プロジェクトの合計遅延時間: 各プロジェクトの所要時間 (メイクスパン) を最短にする。
ソフト制約:
- メイクスパン合計: 複数のプロジェクトスケジュールの合計所要時間を最短にする。
この問題は MISTA 2013 challenge で定義されています。
3.3.4.2. 問題の規模
Schedule A-1 has 2 projects, 24 jobs, 64 execution modes, 7 resources and 150 resource requirements. Schedule A-2 has 2 projects, 44 jobs, 124 execution modes, 7 resources and 420 resource requirements. Schedule A-3 has 2 projects, 64 jobs, 184 execution modes, 7 resources and 630 resource requirements. Schedule A-4 has 5 projects, 60 jobs, 160 execution modes, 16 resources and 390 resource requirements. Schedule A-5 has 5 projects, 110 jobs, 310 execution modes, 16 resources and 900 resource requirements. Schedule A-6 has 5 projects, 160 jobs, 460 execution modes, 16 resources and 1440 resource requirements. Schedule A-7 has 10 projects, 120 jobs, 320 execution modes, 22 resources and 900 resource requirements. Schedule A-8 has 10 projects, 220 jobs, 620 execution modes, 22 resources and 1860 resource requirements. Schedule A-9 has 10 projects, 320 jobs, 920 execution modes, 31 resources and 2880 resource requirements. Schedule A-10 has 10 projects, 320 jobs, 920 execution modes, 31 resources and 2970 resource requirements. Schedule B-1 has 10 projects, 120 jobs, 320 execution modes, 31 resources and 900 resource requirements. Schedule B-2 has 10 projects, 220 jobs, 620 execution modes, 22 resources and 1740 resource requirements. Schedule B-3 has 10 projects, 320 jobs, 920 execution modes, 31 resources and 3060 resource requirements. Schedule B-4 has 15 projects, 180 jobs, 480 execution modes, 46 resources and 1530 resource requirements. Schedule B-5 has 15 projects, 330 jobs, 930 execution modes, 46 resources and 2760 resource requirements. Schedule B-6 has 15 projects, 480 jobs, 1380 execution modes, 46 resources and 4500 resource requirements. Schedule B-7 has 20 projects, 240 jobs, 640 execution modes, 61 resources and 1710 resource requirements. Schedule B-8 has 20 projects, 440 jobs, 1240 execution modes, 42 resources and 3180 resource requirements. Schedule B-9 has 20 projects, 640 jobs, 1840 execution modes, 61 resources and 5940 resource requirements. Schedule B-10 has 20 projects, 460 jobs, 1300 execution modes, 42 resources and 4260 resource requirements.
3.3.5. 病床計画 (PAS - 入院スケジュール)
3.3.5.1. 問題の詳細
(入院予定の) 各患者に、入院時のベッドを割り当てます。各ベッドは病室に所属し、各病室は診療科部門に所属します。患者の入院日と退院日は固定されており、入院日のベッド割り当てだけを行う必要があります。
この問題は 過制約 データセットを使用しています。
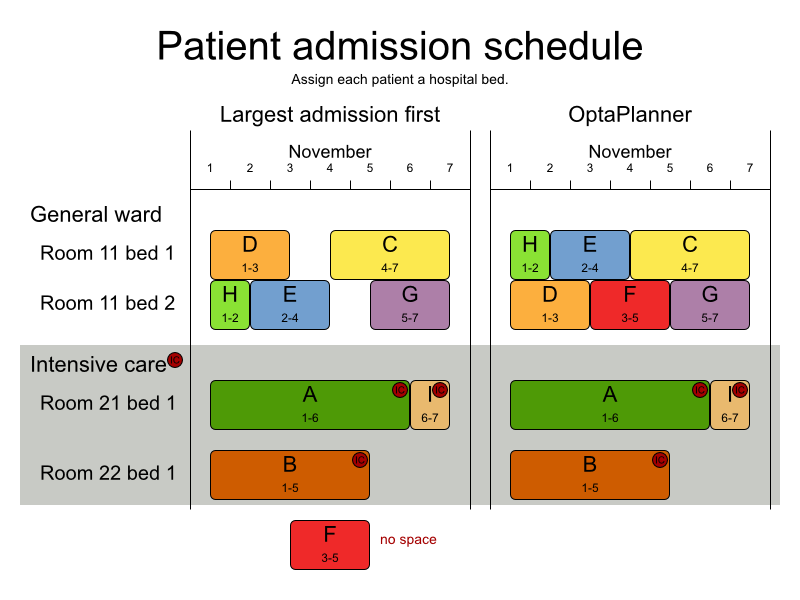
ハード制約:
-
患者 2 名を、同じ日に、同じベッドに割り当てることはできない。重み
-1000hard * conflictNightCount -
病室には、性別の制約を加えることができる: 1 晩に割り当てる性別を女性のみ、または男性のみ (もしくは、性別の制約なし) に設定できる。重み:
-50hard * nightCount -
部門には、年齢の上限または下限を設定できる。重み:
-100hard * nightCount -
患者は、特定の設備のある病室をリクエストできる。重み:
-50hard * nightCount
中程度の制約:
-
データセットに制約を過剰に課さない場合は、すべての患者にベッドを割り当てる。重み:
-1medium * nightCount
ソフト制約:
-
患者は、最大の病室サイズ (例: 一人部屋など) を選択できる。重み:
-8soft * nightCount -
患者は、その病状を専門とする診療科部門にできるだけ割り当てる。重み:
-10soft * nightCount 患者は、その病状を専門とする病室にできるだけ割り当てる。重み:
-20soft * nightCount-
病室の専門科の優先順位を 1 とする。重み:
-10soft * (priority - 1) * nightCount
-
病室の専門科の優先順位を 1 とする。重み:
-
患者は特定の設備のある病室を希望することができる。重み:
-50hard * nightCount
この問題は、Kaho Patient Scheduling に変更を加えたもので、データセットは病院から提供された実際のデータを使用しています。
3.3.5.2. 問題の規模
testdata01 has 4 specialisms, 2 equipments, 4 departments, 98 rooms, 286 beds, 14 nights, 652 patients and 652 admissions with a search space of 10^1601. testdata02 has 6 specialisms, 2 equipments, 6 departments, 151 rooms, 465 beds, 14 nights, 755 patients and 755 admissions with a search space of 10^2013. testdata03 has 5 specialisms, 2 equipments, 5 departments, 131 rooms, 395 beds, 14 nights, 708 patients and 708 admissions with a search space of 10^1838. testdata04 has 6 specialisms, 2 equipments, 6 departments, 155 rooms, 471 beds, 14 nights, 746 patients and 746 admissions with a search space of 10^1994. testdata05 has 4 specialisms, 2 equipments, 4 departments, 102 rooms, 325 beds, 14 nights, 587 patients and 587 admissions with a search space of 10^1474. testdata06 has 4 specialisms, 2 equipments, 4 departments, 104 rooms, 313 beds, 14 nights, 685 patients and 685 admissions with a search space of 10^1709. testdata07 has 6 specialisms, 4 equipments, 6 departments, 162 rooms, 472 beds, 14 nights, 519 patients and 519 admissions with a search space of 10^1387. testdata08 has 6 specialisms, 4 equipments, 6 departments, 148 rooms, 441 beds, 21 nights, 895 patients and 895 admissions with a search space of 10^2366. testdata09 has 4 specialisms, 4 equipments, 4 departments, 105 rooms, 310 beds, 28 nights, 1400 patients and 1400 admissions with a search space of 10^3487. testdata10 has 4 specialisms, 4 equipments, 4 departments, 104 rooms, 308 beds, 56 nights, 1575 patients and 1575 admissions with a search space of 10^3919. testdata11 has 4 specialisms, 4 equipments, 4 departments, 107 rooms, 318 beds, 91 nights, 2514 patients and 2514 admissions with a search space of 10^6291. testdata12 has 4 specialisms, 4 equipments, 4 departments, 105 rooms, 310 beds, 84 nights, 2750 patients and 2750 admissions with a search space of 10^6851. testdata13 has 5 specialisms, 4 equipments, 5 departments, 125 rooms, 368 beds, 28 nights, 907 patients and 1109 admissions with a search space of 10^2845.
3.3.5.3. ドメインモデル
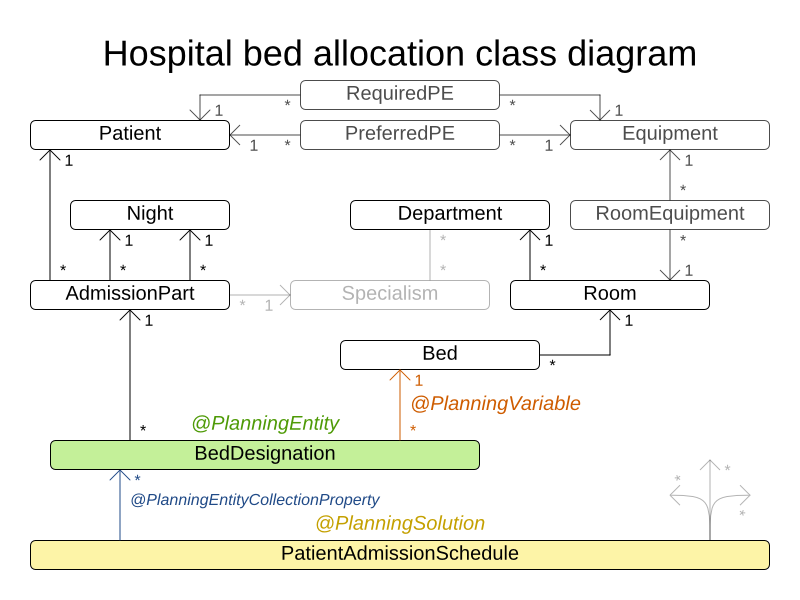
3.4. 複雑な例
3.4.1. 試験の時間割 (ITC 2007 track 1 - 試験)
3.4.1.1. 問題の詳細
すべての試験に、時間と部屋を割り当てます。同じ時間帯の同じ部屋で、複数の試験を行うことができるものとします。
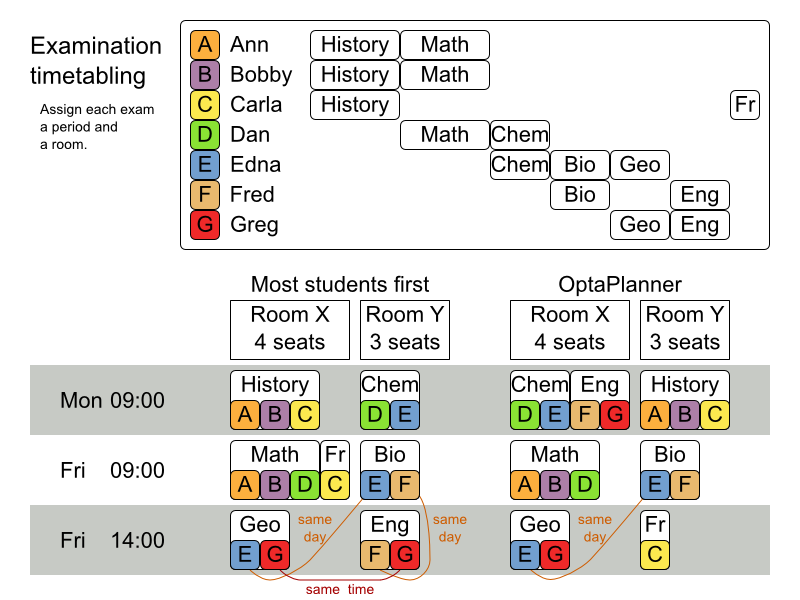
ハード制約:
- 試験の制約: 同じ学生が受ける 2 つの試験は、同じ時間帯に実施できないものとする。
- 教室の収容人数: 教室の座席数は、常に受験者数よりも多くなければならない。
- 期間: 期間は、すべての試験に対応できる長さでなければならない。
期間関連のハード制約 (データセットごとに指定):
- 一致: 特定の 2 つの試験を同じ時間帯に設定する必要がある (別の教室を使用することも可能)。
- 除外: 特定の 2 つの試験を同じ時間帯に設定できない。
- 以降: 特定の試験を、特定の試験の後に行う必要がある。
教室関連の制約 (データセット毎ごとに指定):
- 排他的: 特定の試験を、他の試験と同じ教室で行うことはできない。
ソフト制約 (パラメーター化されたペナルティーがそれぞれ設定されている):
- 同じ学生が、続けて試験を 2 つ受けてはいけない。
- 同じ学生が、同じ日に試験を 2 つ受けてはいけない。
- 時間帯の分散: 同じ学生が受ける 2 つの試験は、時間をある程度あける。
- 異なる試験の長さ: 教室を共有する 2 つの試験の長さは、同じにする。
- 前倒し: 規模の大きい試験は、スケジュールを早めに決定する。
- 期間のペナルティー (データセットごとに指定): 期間によっては、使用されるとペナルティーが発生する。
- 部屋のペナルティー (データセットごとに指定): 部屋によっては、使用されるとペナルティーが発生する。
大学から取得した試験の大規模データセットを使用します。
この問題は International Timetabling Competition 2007 track 1 で明示されました。Geoffrey De Smet 氏は、ごく初期段階の Planner を使用して、このコンペティションで 4 位を獲得しました。このコンペティション以降、多くの改良点が加えられています。
3.4.1.2. 問題の規模
exam_comp_set1 has 7883 students, 607 exams, 54 periods, 7 rooms, 12 period constraints and 0 room constraints with a search space of 10^1564. exam_comp_set2 has 12484 students, 870 exams, 40 periods, 49 rooms, 12 period constraints and 2 room constraints with a search space of 10^2864. exam_comp_set3 has 16365 students, 934 exams, 36 periods, 48 rooms, 168 period constraints and 15 room constraints with a search space of 10^3023. exam_comp_set4 has 4421 students, 273 exams, 21 periods, 1 rooms, 40 period constraints and 0 room constraints with a search space of 10^360. exam_comp_set5 has 8719 students, 1018 exams, 42 periods, 3 rooms, 27 period constraints and 0 room constraints with a search space of 10^2138. exam_comp_set6 has 7909 students, 242 exams, 16 periods, 8 rooms, 22 period constraints and 0 room constraints with a search space of 10^509. exam_comp_set7 has 13795 students, 1096 exams, 80 periods, 15 rooms, 28 period constraints and 0 room constraints with a search space of 10^3374. exam_comp_set8 has 7718 students, 598 exams, 80 periods, 8 rooms, 20 period constraints and 1 room constraints with a search space of 10^1678.
3.4.1.3. ドメインモデル
以下に、主な試験のドメインクラスを紹介しています。
図3.3 試験のドメインクラスの図
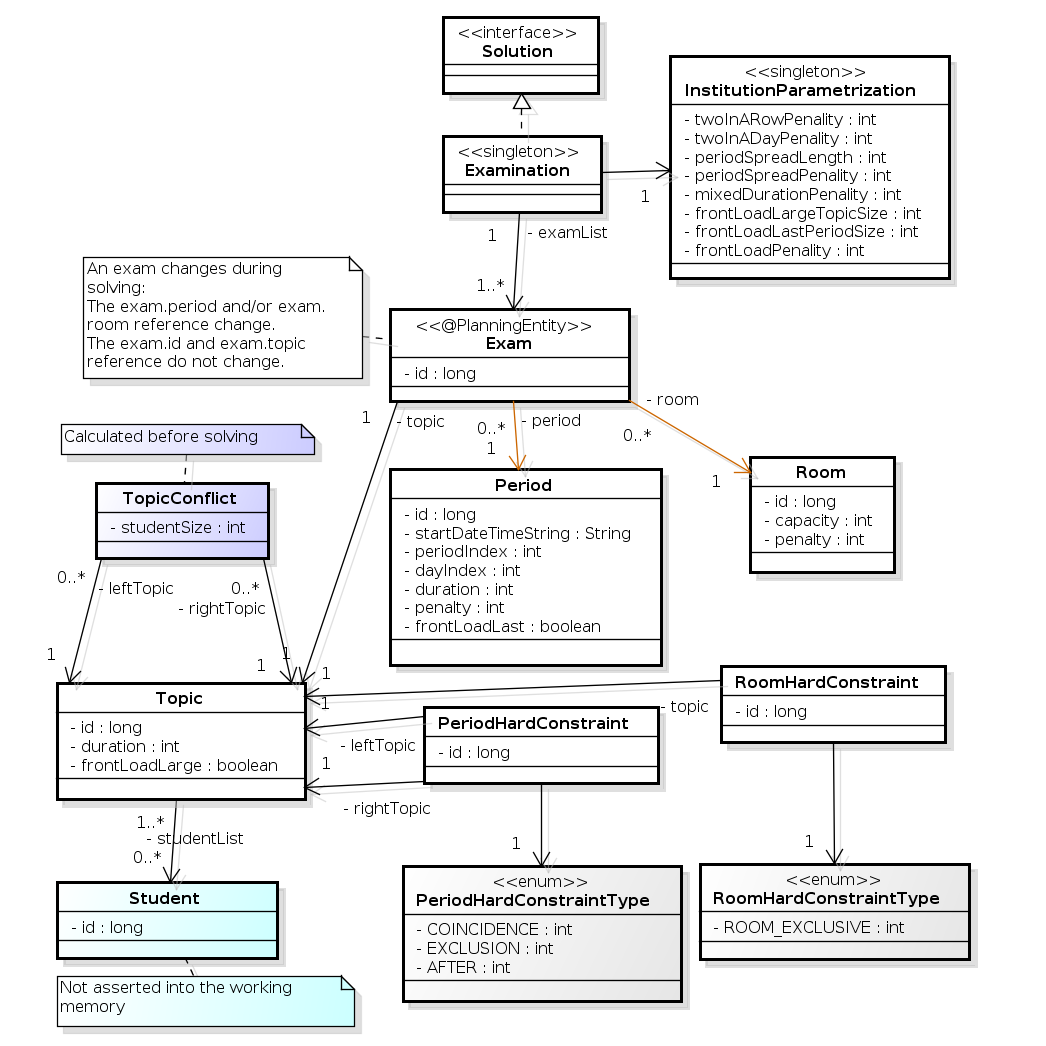
試験のコンセプトを、Exam クラスと Topic クラスに分けた点に注意してください。期間または教室のプロパティーを変更し、ソリューション (プランニングエンティティークラス) を求めると、Exam インスタンスが変化します。このとき、Topic インスタンス、Period インスタンス、および Room インスタンスは変化しません (他のクラスと同様、これらも問題ファクトです)。
3.4.2. 従業員の勤務表 (INRC 2010 - 看護師の勤務表)
3.4.2.1. 問題の詳細
各シフトに看護師を割り当てます。
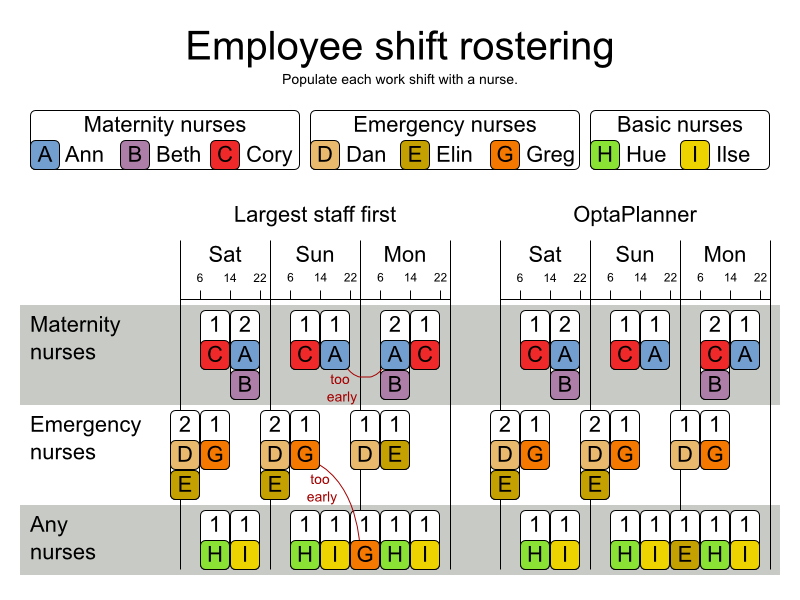
ハード制約:
- 未割り当てのシフトなし (組み込み): すべてのシフトを従業員に割り当てる必要がある。
- シフトの制約: 従業員には 1 日に 1 シフトだけ割り当てることができる。
ソフト制約:
契約上の義務: この業界では、頻繁に契約上の義務に違反するため、ハード制約ではなく、ソフト制約として定義することに決定しました。
- 割り当ての下限および上限: 各従業員は、(それぞれの契約に合わせて) x より多く、y よりも少ないシフト数を勤務する必要がある。
- 連続勤務日数の下限および上限: 各従業員は、(それぞれの契約に合わせて) 連続で x 日から y 日間、勤務する必要がある。
- 連続公休日数の下限および上限: 各従業員は、(それぞれの契約に合わせて) 連続で x 日から y 日間、休む必要がある。
- 週末に連続勤務する回数の下限および上限: 各従業員は、(それぞれの契約に合わせて) 連続で x 回から y 回、週末勤務する必要がある。
- 週末の勤務有無を同じにする: 各従業員は、週末の両日を勤務する、または休む必要がある。
- 週末のシフトタイプを同じにする: 各従業員に、同じ週末のシフトタイプは、同じにする必要がある。
- 好ましくないシフトパターン: 遅番＋早番＋遅番など、好ましくないシフトタイプを連続で組み合わせたパターン。
従業員の希望:
- 勤務日のリクエスト: 従業員は、特定の勤務希望日を申請できる。
- 公休日のリクエスト: 従業員は、特定の公休希望日を申請できる。
- 勤務するシフトのリクエスト: 従業員は特定のシフトへの割り当てを希望できる。
- 勤務しないシフトのリクエスト: 従業員は特定のシフトに割り当てられないように希望できる。
- 他のスキル: シフトに割り当てられた従業員は、そのシフトで必要な全スキルに堪能である必要がある。
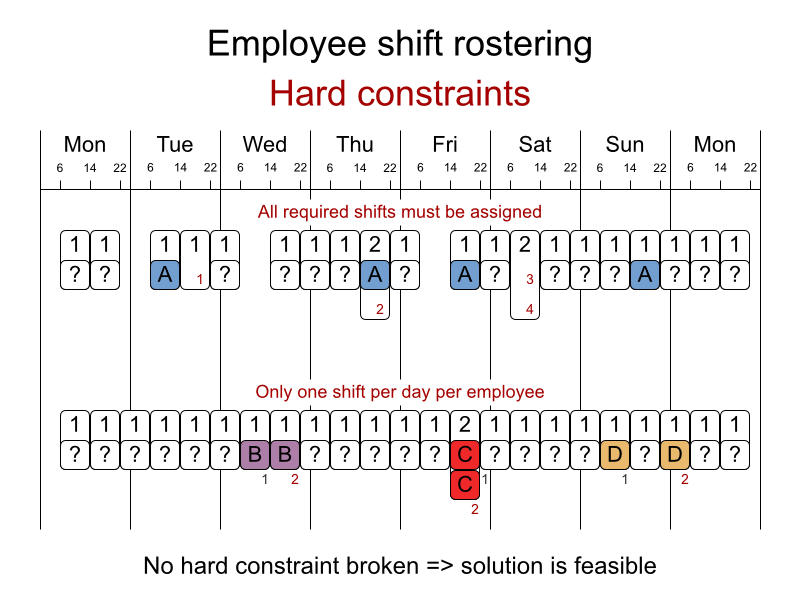
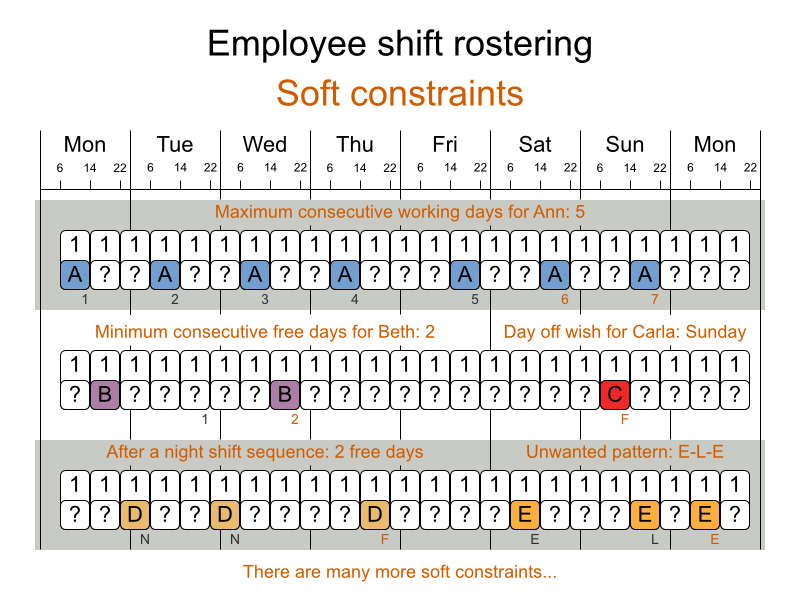
この問題は International Nurse Rostering Competition 2010 で定義されています。
3.4.2.2. 問題の規模
以下のように、データセットの種類は 3 つあります。
- sprint: 数秒で問題を解決する必要があります。
- medium: 数分で問題を解決する必要があります。
- long: 数時間で問題を解決する必要があります。
toy1 has 1 skills, 3 shiftTypes, 2 patterns, 1 contracts, 6 employees, 7 shiftDates, 35 shiftAssignments and 0 requests with a search space of 10^27. toy2 has 1 skills, 3 shiftTypes, 3 patterns, 2 contracts, 20 employees, 28 shiftDates, 180 shiftAssignments and 140 requests with a search space of 10^234. sprint01 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint02 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint03 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint04 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint05 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint06 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint07 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint08 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint09 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint10 has 1 skills, 4 shiftTypes, 3 patterns, 4 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_hint01 has 1 skills, 4 shiftTypes, 8 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_hint02 has 1 skills, 4 shiftTypes, 0 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_hint03 has 1 skills, 4 shiftTypes, 8 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_late01 has 1 skills, 4 shiftTypes, 8 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_late02 has 1 skills, 3 shiftTypes, 4 patterns, 3 contracts, 10 employees, 28 shiftDates, 144 shiftAssignments and 139 requests with a search space of 10^144. sprint_late03 has 1 skills, 4 shiftTypes, 8 patterns, 3 contracts, 10 employees, 28 shiftDates, 160 shiftAssignments and 150 requests with a search space of 10^160. sprint_late04 has 1 skills, 4 shiftTypes, 8 patterns, 3 contracts, 10 employees, 28 shiftDates, 160 shiftAssignments and 150 requests with a search space of 10^160. sprint_late05 has 1 skills, 4 shiftTypes, 8 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_late06 has 1 skills, 4 shiftTypes, 0 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_late07 has 1 skills, 4 shiftTypes, 0 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. sprint_late08 has 1 skills, 4 shiftTypes, 0 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 0 requests with a search space of 10^152. sprint_late09 has 1 skills, 4 shiftTypes, 0 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 0 requests with a search space of 10^152. sprint_late10 has 1 skills, 4 shiftTypes, 0 patterns, 3 contracts, 10 employees, 28 shiftDates, 152 shiftAssignments and 150 requests with a search space of 10^152. medium01 has 1 skills, 4 shiftTypes, 0 patterns, 4 contracts, 31 employees, 28 shiftDates, 608 shiftAssignments and 403 requests with a search space of 10^906. medium02 has 1 skills, 4 shiftTypes, 0 patterns, 4 contracts, 31 employees, 28 shiftDates, 608 shiftAssignments and 403 requests with a search space of 10^906. medium03 has 1 skills, 4 shiftTypes, 0 patterns, 4 contracts, 31 employees, 28 shiftDates, 608 shiftAssignments and 403 requests with a search space of 10^906. medium04 has 1 skills, 4 shiftTypes, 0 patterns, 4 contracts, 31 employees, 28 shiftDates, 608 shiftAssignments and 403 requests with a search space of 10^906. medium05 has 1 skills, 4 shiftTypes, 0 patterns, 4 contracts, 31 employees, 28 shiftDates, 608 shiftAssignments and 403 requests with a search space of 10^906. medium_hint01 has 1 skills, 4 shiftTypes, 7 patterns, 4 contracts, 30 employees, 28 shiftDates, 428 shiftAssignments and 390 requests with a search space of 10^632. medium_hint02 has 1 skills, 4 shiftTypes, 7 patterns, 3 contracts, 30 employees, 28 shiftDates, 428 shiftAssignments and 390 requests with a search space of 10^632. medium_hint03 has 1 skills, 4 shiftTypes, 7 patterns, 4 contracts, 30 employees, 28 shiftDates, 428 shiftAssignments and 390 requests with a search space of 10^632. medium_late01 has 1 skills, 4 shiftTypes, 7 patterns, 4 contracts, 30 employees, 28 shiftDates, 424 shiftAssignments and 390 requests with a search space of 10^626. medium_late02 has 1 skills, 4 shiftTypes, 7 patterns, 3 contracts, 30 employees, 28 shiftDates, 428 shiftAssignments and 390 requests with a search space of 10^632. medium_late03 has 1 skills, 4 shiftTypes, 0 patterns, 4 contracts, 30 employees, 28 shiftDates, 428 shiftAssignments and 390 requests with a search space of 10^632. medium_late04 has 1 skills, 4 shiftTypes, 7 patterns, 3 contracts, 30 employees, 28 shiftDates, 416 shiftAssignments and 390 requests with a search space of 10^614. medium_late05 has 2 skills, 5 shiftTypes, 7 patterns, 4 contracts, 30 employees, 28 shiftDates, 452 shiftAssignments and 390 requests with a search space of 10^667. long01 has 2 skills, 5 shiftTypes, 3 patterns, 3 contracts, 49 employees, 28 shiftDates, 740 shiftAssignments and 735 requests with a search space of 10^1250. long02 has 2 skills, 5 shiftTypes, 3 patterns, 3 contracts, 49 employees, 28 shiftDates, 740 shiftAssignments and 735 requests with a search space of 10^1250. long03 has 2 skills, 5 shiftTypes, 3 patterns, 3 contracts, 49 employees, 28 shiftDates, 740 shiftAssignments and 735 requests with a search space of 10^1250. long04 has 2 skills, 5 shiftTypes, 3 patterns, 3 contracts, 49 employees, 28 shiftDates, 740 shiftAssignments and 735 requests with a search space of 10^1250. long05 has 2 skills, 5 shiftTypes, 3 patterns, 3 contracts, 49 employees, 28 shiftDates, 740 shiftAssignments and 735 requests with a search space of 10^1250. long_hint01 has 2 skills, 5 shiftTypes, 9 patterns, 3 contracts, 50 employees, 28 shiftDates, 740 shiftAssignments and 0 requests with a search space of 10^1257. long_hint02 has 2 skills, 5 shiftTypes, 7 patterns, 3 contracts, 50 employees, 28 shiftDates, 740 shiftAssignments and 0 requests with a search space of 10^1257. long_hint03 has 2 skills, 5 shiftTypes, 7 patterns, 3 contracts, 50 employees, 28 shiftDates, 740 shiftAssignments and 0 requests with a search space of 10^1257. long_late01 has 2 skills, 5 shiftTypes, 9 patterns, 3 contracts, 50 employees, 28 shiftDates, 752 shiftAssignments and 0 requests with a search space of 10^1277. long_late02 has 2 skills, 5 shiftTypes, 9 patterns, 4 contracts, 50 employees, 28 shiftDates, 752 shiftAssignments and 0 requests with a search space of 10^1277. long_late03 has 2 skills, 5 shiftTypes, 9 patterns, 3 contracts, 50 employees, 28 shiftDates, 752 shiftAssignments and 0 requests with a search space of 10^1277. long_late04 has 2 skills, 5 shiftTypes, 9 patterns, 4 contracts, 50 employees, 28 shiftDates, 752 shiftAssignments and 0 requests with a search space of 10^1277. long_late05 has 2 skills, 5 shiftTypes, 9 patterns, 3 contracts, 50 employees, 28 shiftDates, 740 shiftAssignments and 0 requests with a search space of 10^1257.
3.4.2.3. ドメインモデル
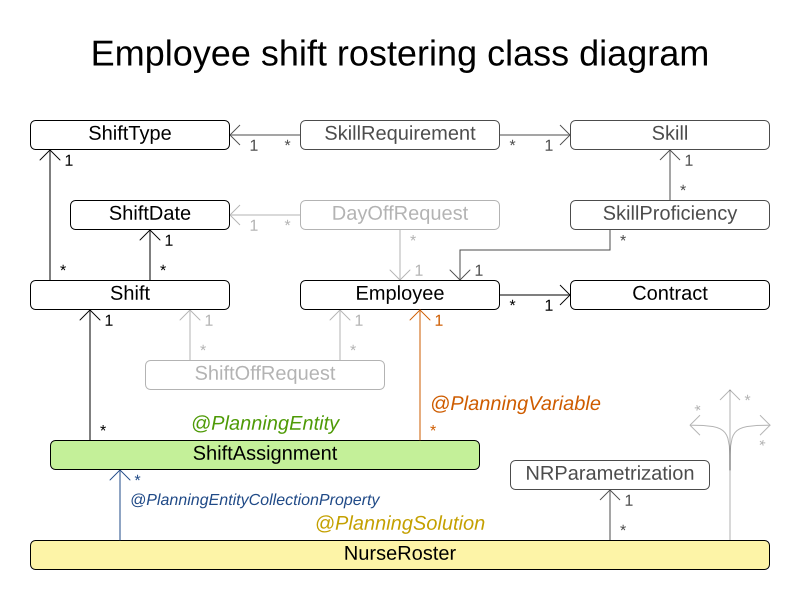
3.4.3. 巡回トーナメント問題 (TTP)
3.4.3.1. 問題の詳細
n チーム間の試合をスケジュールします。
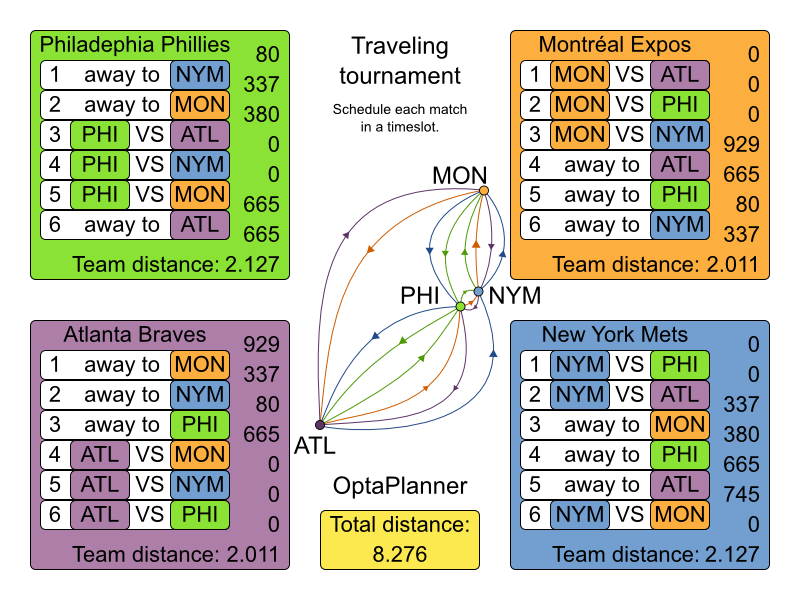
ハード制約:
- 各チームは、他のチームとそれぞれ 2 回 (ホームとアウェイ) 試合をする。
- 各チームは、各時間枠に 1 試合だけ行う。
- 3 回連続で、ホームまたはアウェイでの試合はできない。
- 繰り返しなし: 同じ対戦相手と 2 回連続で対戦できない。
ソフト制約:
- 全チームが移動する合計距離を最小限に抑える。
この問題は Michael Trick の Web サイト (世界記録が含まれます) で定義されています。
3.4.3.2. 問題の規模
1-nl04 has 6 days, 4 teams and 12 matches with a search space of 10^9. 1-nl06 has 10 days, 6 teams and 30 matches with a search space of 10^30. 1-nl08 has 14 days, 8 teams and 56 matches with a search space of 10^64. 1-nl10 has 18 days, 10 teams and 90 matches with a search space of 10^112. 1-nl12 has 22 days, 12 teams and 132 matches with a search space of 10^177. 1-nl14 has 26 days, 14 teams and 182 matches with a search space of 10^257. 1-nl16 has 30 days, 16 teams and 240 matches with a search space of 10^354. 2-bra24 has 46 days, 24 teams and 552 matches with a search space of 10^917. 3-nfl16 has 30 days, 16 teams and 240 matches with a search space of 10^354. 3-nfl18 has 34 days, 18 teams and 306 matches with a search space of 10^468. 3-nfl20 has 38 days, 20 teams and 380 matches with a search space of 10^600. 3-nfl22 has 42 days, 22 teams and 462 matches with a search space of 10^749. 3-nfl24 has 46 days, 24 teams and 552 matches with a search space of 10^917. 3-nfl26 has 50 days, 26 teams and 650 matches with a search space of 10^1104. 3-nfl28 has 54 days, 28 teams and 756 matches with a search space of 10^1309. 3-nfl30 has 58 days, 30 teams and 870 matches with a search space of 10^1534. 3-nfl32 has 62 days, 32 teams and 992 matches with a search space of 10^1778. 4-super04 has 6 days, 4 teams and 12 matches with a search space of 10^9. 4-super06 has 10 days, 6 teams and 30 matches with a search space of 10^30. 4-super08 has 14 days, 8 teams and 56 matches with a search space of 10^64. 4-super10 has 18 days, 10 teams and 90 matches with a search space of 10^112. 4-super12 has 22 days, 12 teams and 132 matches with a search space of 10^177. 4-super14 has 26 days, 14 teams and 182 matches with a search space of 10^257. 5-galaxy04 has 6 days, 4 teams and 12 matches with a search space of 10^9. 5-galaxy06 has 10 days, 6 teams and 30 matches with a search space of 10^30. 5-galaxy08 has 14 days, 8 teams and 56 matches with a search space of 10^64. 5-galaxy10 has 18 days, 10 teams and 90 matches with a search space of 10^112. 5-galaxy12 has 22 days, 12 teams and 132 matches with a search space of 10^177. 5-galaxy14 has 26 days, 14 teams and 182 matches with a search space of 10^257. 5-galaxy16 has 30 days, 16 teams and 240 matches with a search space of 10^354. 5-galaxy18 has 34 days, 18 teams and 306 matches with a search space of 10^468. 5-galaxy20 has 38 days, 20 teams and 380 matches with a search space of 10^600. 5-galaxy22 has 42 days, 22 teams and 462 matches with a search space of 10^749. 5-galaxy24 has 46 days, 24 teams and 552 matches with a search space of 10^917. 5-galaxy26 has 50 days, 26 teams and 650 matches with a search space of 10^1104. 5-galaxy28 has 54 days, 28 teams and 756 matches with a search space of 10^1309. 5-galaxy30 has 58 days, 30 teams and 870 matches with a search space of 10^1534. 5-galaxy32 has 62 days, 32 teams and 992 matches with a search space of 10^1778. 5-galaxy34 has 66 days, 34 teams and 1122 matches with a search space of 10^2041. 5-galaxy36 has 70 days, 36 teams and 1260 matches with a search space of 10^2324. 5-galaxy38 has 74 days, 38 teams and 1406 matches with a search space of 10^2628. 5-galaxy40 has 78 days, 40 teams and 1560 matches with a search space of 10^2951.
3.4.4. コストを抑えるスケジュール
3.4.4.1. 問題の詳細
全タスクを時間内にスケジュールし、機械の電気代を最小限に抑えます。電気代は時間によって異なります。これは、ジョブショップスケジューリング の応用です。
ハード制約:
- 開始時間の制限: 各タスクは、最早と最遅の開始時間の制限内に、開始する必要がある。
- 最大容量: 各機械に割り当てる各リソースは最大容量を超過することはできない。
- 開始および終了: 各機械は、タスクが割り当てられている間は稼働している必要がある。次のタスクまでの間、起動および終了コストを避けるため、機械をアイドルにすることができる。
中程度の制約:
電気代: 全スケジュールの合計電気代を最小限に抑える。
- 機械の電気代: 稼働中またはアイドル中の機械はそれぞれ、電気を消費し、電気代が発生する (金額は使用時の電気代によって異なる)。
- タスクの電気代: 各タスクも電気を消費し、電気代が発生する (金額は使用時の電気代によって異なる)。
- 機械の起動および終了コスト: 機械を起動または終了するたびに、追加のコストが発生する。
ソフト制約 (問題に元々設定されている定義に追加):
- 早く開始: なるべく早めにタスクを開始するようにする。
この問題は ICON challenge で定義されています。
3.4.4.2. 問題の規模
sample01 has 3 resources, 2 machines, 288 periods and 25 tasks with a search space of 10^53. sample02 has 3 resources, 2 machines, 288 periods and 50 tasks with a search space of 10^114. sample03 has 3 resources, 2 machines, 288 periods and 100 tasks with a search space of 10^226. sample04 has 3 resources, 5 machines, 288 periods and 100 tasks with a search space of 10^266. sample05 has 3 resources, 2 machines, 288 periods and 250 tasks with a search space of 10^584. sample06 has 3 resources, 5 machines, 288 periods and 250 tasks with a search space of 10^673. sample07 has 3 resources, 2 machines, 288 periods and 1000 tasks with a search space of 10^2388. sample08 has 3 resources, 5 machines, 288 periods and 1000 tasks with a search space of 10^2748. sample09 has 4 resources, 20 machines, 288 periods and 2000 tasks with a search space of 10^6668. instance00 has 1 resources, 10 machines, 288 periods and 200 tasks with a search space of 10^595. instance01 has 1 resources, 10 machines, 288 periods and 200 tasks with a search space of 10^599. instance02 has 1 resources, 10 machines, 288 periods and 200 tasks with a search space of 10^599. instance03 has 1 resources, 10 machines, 288 periods and 200 tasks with a search space of 10^591. instance04 has 1 resources, 10 machines, 288 periods and 200 tasks with a search space of 10^590. instance05 has 2 resources, 25 machines, 288 periods and 200 tasks with a search space of 10^667. instance06 has 2 resources, 25 machines, 288 periods and 200 tasks with a search space of 10^660. instance07 has 2 resources, 25 machines, 288 periods and 200 tasks with a search space of 10^662. instance08 has 2 resources, 25 machines, 288 periods and 200 tasks with a search space of 10^651. instance09 has 2 resources, 25 machines, 288 periods and 200 tasks with a search space of 10^659. instance10 has 2 resources, 20 machines, 288 periods and 500 tasks with a search space of 10^1657. instance11 has 2 resources, 20 machines, 288 periods and 500 tasks with a search space of 10^1644. instance12 has 2 resources, 20 machines, 288 periods and 500 tasks with a search space of 10^1637. instance13 has 2 resources, 20 machines, 288 periods and 500 tasks with a search space of 10^1659. instance14 has 2 resources, 20 machines, 288 periods and 500 tasks with a search space of 10^1643. instance15 has 3 resources, 40 machines, 288 periods and 500 tasks with a search space of 10^1782. instance16 has 3 resources, 40 machines, 288 periods and 500 tasks with a search space of 10^1778. instance17 has 3 resources, 40 machines, 288 periods and 500 tasks with a search space of 10^1764. instance18 has 3 resources, 40 machines, 288 periods and 500 tasks with a search space of 10^1769. instance19 has 3 resources, 40 machines, 288 periods and 500 tasks with a search space of 10^1778. instance20 has 3 resources, 50 machines, 288 periods and 1000 tasks with a search space of 10^3689. instance21 has 3 resources, 50 machines, 288 periods and 1000 tasks with a search space of 10^3678. instance22 has 3 resources, 50 machines, 288 periods and 1000 tasks with a search space of 10^3706. instance23 has 3 resources, 50 machines, 288 periods and 1000 tasks with a search space of 10^3676. instance24 has 3 resources, 50 machines, 288 periods and 1000 tasks with a search space of 10^3681. instance25 has 3 resources, 60 machines, 288 periods and 1000 tasks with a search space of 10^3774. instance26 has 3 resources, 60 machines, 288 periods and 1000 tasks with a search space of 10^3737. instance27 has 3 resources, 60 machines, 288 periods and 1000 tasks with a search space of 10^3744. instance28 has 3 resources, 60 machines, 288 periods and 1000 tasks with a search space of 10^3731. instance29 has 3 resources, 60 machines, 288 periods and 1000 tasks with a search space of 10^3746. instance30 has 4 resources, 70 machines, 288 periods and 2000 tasks with a search space of 10^7718. instance31 has 4 resources, 70 machines, 288 periods and 2000 tasks with a search space of 10^7740. instance32 has 4 resources, 70 machines, 288 periods and 2000 tasks with a search space of 10^7686. instance33 has 4 resources, 70 machines, 288 periods and 2000 tasks with a search space of 10^7672. instance34 has 4 resources, 70 machines, 288 periods and 2000 tasks with a search space of 10^7695. instance35 has 4 resources, 80 machines, 288 periods and 2000 tasks with a search space of 10^7807. instance36 has 4 resources, 80 machines, 288 periods and 2000 tasks with a search space of 10^7814. instance37 has 4 resources, 80 machines, 288 periods and 2000 tasks with a search space of 10^7764. instance38 has 4 resources, 80 machines, 288 periods and 2000 tasks with a search space of 10^7736. instance39 has 4 resources, 80 machines, 288 periods and 2000 tasks with a search space of 10^7783. instance40 has 4 resources, 90 machines, 288 periods and 4000 tasks with a search space of 10^15976. instance41 has 4 resources, 90 machines, 288 periods and 4000 tasks with a search space of 10^15935. instance42 has 4 resources, 90 machines, 288 periods and 4000 tasks with a search space of 10^15887. instance43 has 4 resources, 90 machines, 288 periods and 4000 tasks with a search space of 10^15896. instance44 has 4 resources, 90 machines, 288 periods and 4000 tasks with a search space of 10^15885. instance45 has 4 resources, 100 machines, 288 periods and 5000 tasks with a search space of 10^20173. instance46 has 4 resources, 100 machines, 288 periods and 5000 tasks with a search space of 10^20132. instance47 has 4 resources, 100 machines, 288 periods and 5000 tasks with a search space of 10^20126. instance48 has 4 resources, 100 machines, 288 periods and 5000 tasks with a search space of 10^20110. instance49 has 4 resources, 100 machines, 288 periods and 5000 tasks with a search space of 10^20078.
3.4.5. 投資資産クラスの割り当て (ポートフォリオの最適化)
3.4.5.1. 問題の詳細
各資産クラスに投資する相対数を決定します。
ハード制約:
リスクの最大値: 標準偏差合計は、標準偏差の最大値を超えてはならない。
- 標準偏差合計の計算は、Markowitz Portfolio Theory を適用した、資産クラスの相対関係を考慮する必要があります。
- 地域の最大値: 地域ごとに数量の最大値がある。
- セクターの最大値: 各セクターに数量の最大値がある。
ソフト制約:
- 期待収益を最大化する。
3.4.5.2. 問題の規模
de_smet_1 has 1 regions, 3 sectors and 11 asset classes with a search space of 10^4. irrinki_1 has 2 regions, 3 sectors and 6 asset classes with a search space of 10^3.
サイズが大きいデータセットは作成/検証されていませんが、問題はないはずです。
